В сепарабельном гильбертовом пространстве исследованы включения
с многозначным возмущением и эволюционными операторами, являющимися
субдифференциалами зависящей от времени собственной выпуклой полунепрерывной
снизу функции. Наряду с исходным включением рассматривается последовательность
аппроксимирующих включений с тем же возмущением и эволюционными операторами,
являющимися субдифференциалами регуляризаций Моро—Иосиды исходной функции.
Показано, что множество достижимости исходного включения является равномерным по
времени пределом в метрике Хаусдорфа последовательности множеств достижимости
аппроксимиру ющих включений. В качестве приложений полученных результатов
рассмотрены примеры управляемых систем с разрывными нелинейностями. Для таких
систем найдены аппроксими рующие последовательности гладких управляемых систем,
для которых проведено численное построение множеств достижимости (рис. 1).
Результат, касающийся аппроксимации множеств достижимости включений и
управляемых систем данного типа, не имеет аналогов в мире.
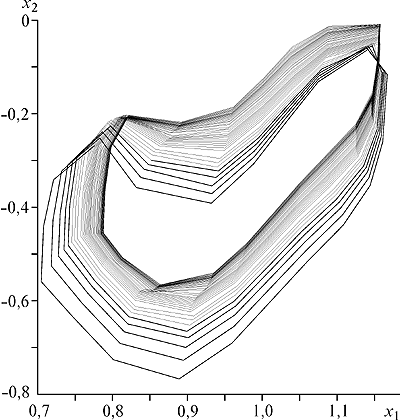 Рис. 1. Результаты расчетов показывают быструю сходимость множеств достижимости аппроксимирующих управляемых систем к множеству достижимости управляемой системы с разрывными нелинейностями.
|


