


| § 1.8. Жесткие системы | 
|
Кто делает большие шаги, не может [долго] идти.
. Дао дэ цзин
Здесь описывается важный и часто встречающийся в приложениях класс так называемых жестких систем дифференциальных уравнений. Изучаются особенности численного решения жестких систем.
1.8.1. Пример. Рассмотрим систему дифференциальных уравнений
| xў1= l1x1, xў2= l2x2, | (1) |
в которой l1 = -1, а l2 = -106. Общее решение этой системы, как известно, имеет вид
| x1(t) = c1e-t, x2(t) = c2e-106t. |
Допустим, нам нужно найти решение (1), удовлетворяющее начальным условиям
| x1(0) = 1, x2(0) = 1. |
Воспользуемся, например, явным методом Эйлера. Поскольку его область устойчивости S (см.
| | l1t + 1| < 1, | l2t + 1| < 1, |
откуда следует, что t должно быть меньше
1.8.2. Жесткие системы.
Описанная выше ситуация возникает из-за большого разброса собственных значений матрицы системы (1):
| xў = Ax | (2) |
называется жесткой, если, во-первых, все собственные значения
|
Число S при этом называют коэффициентом жесткости системы (2). Значок
В случае общей системы дифференциальных уравнений (E) жесткие системы можно выделять по-разному. Наиболее простым определением является, по-видимому, следующее. Пусть
| xў = A(s)x |
Подчеркнем, что понятие жесткости относится к дифференциальному уравнению, а не к разностной схеме.
1.8.3. Еще один пример.
Попытаемся решить систему (1) неявным методом Эйлера. Как мы знаем (см. п. 1.7.7), его область устойчивости представляет собой внешность единичного круга в C с центром в точке +1: в
частности, она содержит всю левую открытую полуплоскость
1.8.4. A-устойчивые методы.
Как упоминалось выше, если область абсолютной устойчивости метода содержит левую открытую полуплоскость
Однако, как оказалось, A-устойчивых методов не так уж много. А именно, доказано, что явных линейных многошаговых A-устойчивых методов (как, впрочем, и явных A-устойчивых методов
Задача 1.8.1. Покажите, что метод трапеций
|
является A-устойчивым методом второго порядка аппроксимации.
1.8.5. A(a)-устойчивые методы.
Из вышеизложенного следует, что требование A-устойчивости резко сужает класс доступных схем. Естественно попытаться снизить требования к области устойчивости метода. Один из возможных вариантов таков. Заметим, что если спектр s(A) матрицы A лежит в левой открытой полуплоскости, в силу своей конечности, он лежит в некотором клине
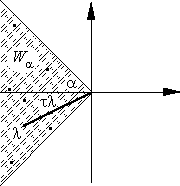
Поэтому, если область абсолютной устойчивости метода содержит клин
Здесь доказано, что не бывает явных даже A(0)-устойчивых методов, но зато для любого
Задача 1.8.2. Покажите, что неявный линейный четырехшаговый метод
| (3) |
является методом четвертого порядка аппроксимации
Задача 1.8.3. Докажите, что метод (3)
A(a)-устойчив при некотором
Отметим, что если заранее известно, что решаемая (устойчивая) система дифференциальных уравнений имеет только вещественные (отрицательные в силу устойчивости) собственные значения (например, если матрица линеаризованной системы симметрична), то для устойчивого счета достаточно уже A(0)-устойчивости метода.
Подчеркнем еще раз, что поскольку, как уже отмечалось, не существует явных даже A(0)-устойчивых методов, для решения жестких задач могут применяться только неявные методы.
В заключение параграфа опишем еще один класс неявных линейных многошаговых методов, активно применяющихся при решении жестких задач.
1.8.6. Методы, основанные на дифференцировании.
В этих методах коэффициенты as, bs линейного многошагового метода подбираются из следующих соображений (ср. c
| Uў(ti-r) = f(ti-r, xi-r). | (4) |
|
и после несложных преобразований равенство (4) превращается в явный метод Эйлера.
Если r = 1, то методы вида (4) явные, если же
Задача 1.8.4. Выведите формулы дифференцирования назад для p = 1, 2, 3.
Задача 1.8.5. Исследуйте область абсолютной устойчивости построенных в предыдущей задаче методов.
При p = 1, 2 формулы дифференцирования назад являются A-устойчивыми, при
File based on translation from
TEX by TTH,
version 3.05.
Created 29 May 2002, 10: 24.