


| § 2.1. Простейшие краевые задачи | 
|
Я не стал бы навязывать читателю всех этих подробностей, если бы не настойчивые расспросы моих земляков.
Генри Дэвид Торо. Уолден, или жизнь в лесу
Из m-параметрического семейства решений уравнения (E) единственное решение можно выделять разными способами. Один из них (начальное условие (C)) мы изучали ранее. Если дополнительные условия задаются в разных точках, то такие задачи называют краевыми. В этом параграфе кратко напоминаются основные понятия теории краевых задач для обыкновенных дифференциальных уравнений.
2.1.1. Постановка краевых задач.
В отличие от теории начальных задач, теория краевых задач для обыкновенных дифференциальных уравнений существенно более сложна и менее завершена. В частности, например, достаточные условия существования и единственности решения краевых задач намного менее продвинуты и далеки от необходимых. Поэтому в данном курсе мы будем рассматривать только простейшую краевую задачу для дифференциального уравнения второго порядка вида
| xўў = f(t, x, xў), t О [0, T], | (E2) |
| x(0) = a, x(T) = b, | (BC) |
в которой f: [0, T]×Rm×Rm ® Rm;
| xўў + A(t)x + B(t)xў = c(t), t О [0, T], | (LE) |
| x(0) = a, x(T) = b, | (BC) |
в которой A(t) и B(t) при каждом
2.1.2. Простейшие условия разрешимости краевой задачи
Приведем в качестве примера одно утверждение о существовании решения указанной задачи. Пусть
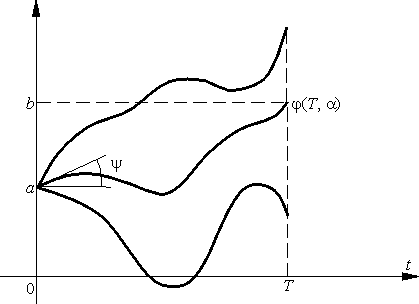
Д о к а з а т е л ь с т в о основывается на так называемом
методе стрельбы. Наряду с задачей
| x(0) = a, xў(0) = a, | (1) |
где a — параметр. Если мы укажем такое значение параметра a, при котором решение
| j(T, a) ® ± Ґ при a ® ±Ґ, | (2) |
то по теореме о промежуточном значении непрерывной функции при некотором a будет выполняться нужное равенство
|
|
|
Учитывая, что |f(t, x, y)| Ј M и, следовательно,
|
получаем (2).
Задача 2.1.1. Восстановите детали доказательства.
Задача 2.1.2. Приведите пример неразрешимой задачи вида
2.1.3. Операторная форма записи задачи
Так же, как и задача
| F(x) = 0, | (OE) |
где F: C2([0, T], Rm) ® C([0, T], Rm)×Rm×Rm и задается формулой
| F(x) = (xўў(·) - f [·, x(·), xў(·)], x(0) - a, x(T) - b). |
2.1.4. О методах решения краевых задач.
Большинство используемых численных методов решения краевых задач может быть отнесено к одному из трех больших классов. Разумеется, границы между этими методами размыты, некоторые методы нельзя отнести ни к одному из этих классов, другие же могут быть отнесены одновременно к двум классам
а) Методы стрельбы. Они основываются в идейном плане на
соображениях, описанных в
б) Конечно-разностные методы, основывающиеся на построении разностных схем, аппроксимирующих решение исходной задачи.
в) Проекционные, или вариационные, методы, суть которых состоит в проектировании исходной задачи на конечномерное пространство функций.
Следующие три параграфа посвящены описанию этих трех классов.
File based on translation from
TEX by TTH,
version 3.05.
Created 30 May 2002, 8: 12.