XIV Международная конференция по интервальной математике
ОЦЕНКА ДОСТОВЕРНОСТИ ЧИСЛЕННЫХ РЕЗУЛЬТАТОВ ПРИ НАЛИЧИИ НЕСКОЛЬКИХ МЕТОДОВ РЕШЕНИЯ ЗАДАЧИ
В.П.Житников, Н.М. Шерыхалина
Уфимский государственный авиационный технический университет, Уфа, Россия
Одной из ключевых проблем численного анализа является разработка средств контроля и доказательства достоверности получаемых результатов, учет всех известных источников погрешности.
Достоверным считается результат, погрешность которого не выходит за предписанные рамки ![]() , где x - точное значение;
, где x - точное значение; ![]() - приближенное значение искомого параметра, полученное численно; e - заданная допустимая величина погрешности. Сложность оценки погрешности и достоверности заключается в том, что возникновение погрешности может быть вызвано различными факторами :
- приближенное значение искомого параметра, полученное численно; e - заданная допустимая величина погрешности. Сложность оценки погрешности и достоверности заключается в том, что возникновение погрешности может быть вызвано различными факторами :
– неадекватностью аналитической и дискретной моделей (заменой производных конечной разностью, интеграла - конечной суммой и т. д.);
– ошибками округления и усечения чисел в машинном представлении;
– ошибками программирования.
Возможность наличия всех этих составляющих погрешности (особенно ошибок программирования, оценить вклад которых весьма затруднительно) в численном результате, полученном при решении достаточно сложной задачи, приводит к неопределенности (размытости) границ интервала возможных значений суммарной погрешности и делает нереальной ее гарантированную оценку. Это приводит к необходимости перехода к вероятностной модели возникновения погрешности. В качестве численной характеристики достоверности будем использовать оценку вероятности того, что фактическая погрешность не выходит за некоторый заданный уровень
![]() (1)
(1)
Для оценки этой вероятности применим следующий подход. Проводится вычисление одного и того же параметра
x несколькими (m) методами, получается несколько приближенных значений yj, j=1,...m. Известными аналитическими и численными способами проводится оценка погрешности каждого результата e j, которую далее будем называть наблюдаемой. Далее путем осреднения находим общую оценку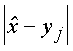 не превосходят e j, то констатируем, что численные данные непротиворечивы.
не превосходят e j, то констатируем, что численные данные непротиворечивы.
Тем не менее в результате этих действий невозможно гарантировать отсутствие дополнительной ненаблюдаемой погрешности у всех полученных значений
yj.Найдем оценку вероятности того, что несмотря на необнаружение ненаблюдаемой погрешности, выходящей за заданные рамки, она все же существует, (это означает, что ненаблюдаемые погрешности всех рассматриваемых методов совпадают с точностью до
s = maxe j). Каждому значению ненаблюдаемой погрешности xk можно приписать некоторую вероятность или рассмотреть функцию распределения f(x). Тогда общая функция плотности вероятности ненаблюдаемой погрешности примет вид![]() (2)
(2)
где
a . - вероятность отсутствия ненаблюдаемой погрешности.Погрешности приближенных значений, полученных разными методами, считаются независимыми случайными величинами. Каждому методу может соответствовать, вообще говоря, своя функция
fk(x), однако, как было показано, результат зависит от произведения этих функций. Поэтому всем методам можно приписать одну и ту же функцию распределения f(x), полученную в результате осреднения fk(x).Вероятность существования ненаблюдаемой погрешности равна вероятности совпадения с точностью
s ненаблюдаемой погрешности xi m методов. Оценка условной вероятности совпадения ненаблюдаемых погрешностей, превышающих некоторую величину e і s , приводит к неравенству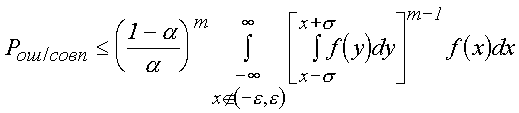 (3)
(3)
Разумную оценку интеграла (3) можно получить, если предположить, что функция
f(x) обладает свойством унимодальности (то есть, если максимум f(x) достигается в точке x0, то при x0<x1<x2 и при x2<x1<x0 f(x0) і f(x1) і f(x2)). Вообще говоря, рассматривая возможные функции распределения погрешности, естественно считать, что меньшие по модулю погрешности встречаются чаще, чем большие. При этом допущении функция f(x) унимодальна, причем точка максимума x0=0. Для таких функций была получена оценка, которую можно записать в виде неравенства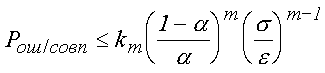 , (4)
, (4)
где
km <1 для mЈ 4.Это позволяют утверждать, что, при уменьшении вычислительной погрешности
s результатов расчетов несколькими способами и их совпадении с этой точностью существенно увеличивается степень их достоверности. Однако, следует отметить, что такой подход требует получения реальных результатов с погрешностью s на один–два порядка меньшей, чем пороговая величина e .При отсутствии статистических оценок величины
a , характеризующей надежность каждого отдельного результата, можно принять a =0.5, согласно гипотезе Лапласа о наибольшей неопределенности. На самом деле, ситуация, в которой a <0.5 означает, что преобладает недоверие к результатам. Это требует проведения дополнительного тестирования с целью поиска ошибки данного метода или программы, которое должно привести либо к локализации и устранению ошибки, либо, если тесты не обнаруживают какого-нибудь несоответствия, к повышению доверия к результату.Таким образом, в данном сообщении предложен способ определения численной характеристики достоверности численных результатов нескольких (2–4) испытаний путем оценки вероятности совпадения погрешностей, вызванных неточностью разных методов и ошибками в программах их реализующих. Показано, что согласно оценке, полученной при достаточно общих условиях, эта вероятность быстро уменьшается при увеличении точности расчетов и числа методов
m. (Отметим, что при обычном статистическом методе оценки ненаблюдаемой погрешности скорость уменьшения неопределенности, независимо от наличия или отсутствия совпадения результатов, обратно пропорциональна m1/2, что требует слишком большого числа различных методов расчета.)