XVI Международная школа-семинар по численным методам механики вязкой жидкости
СТАЦИОНАРНЫЕ ЗАДАЧИ ГРАНИЧНОГО УПРАВЛЕНИЯ ДЛЯ УРАВНЕНИЙ ГИДРОДИНАМИКИ ТЕПЛОПРОВОДНОЙ ЖИДКОСТИ
Г.В. Алексеев*, Э.А. Адомавичюс
Институт прикладной математики
Дальневосточного отделения Российской Академии наук
ул. Радио 7, Владивосток, 690041, Россия
E-mail: alekseev@ipm.marine.su
В работе рассматриваются экстремальные задачи для стационарных уравнений гидродинамики вязкой теплопроводной жидкости. Указанные задачи формулируются как задачи минимизации определенных функционалов качества на слабых решениях соответствующей краевой задачи. В качестве математической модели выступает стационарная система уравнений Обербека-Буссинеска
![]()
![]()
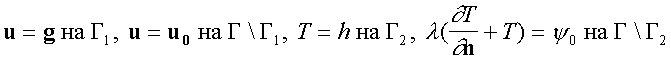 . (1)
. (1)
Здесь используются общепринятые обозначения (см. [1]). В частности,
u, p и T обозначают поля скорости, давления и температуры, функции g наВ качестве функционалов качества выбираются следующие
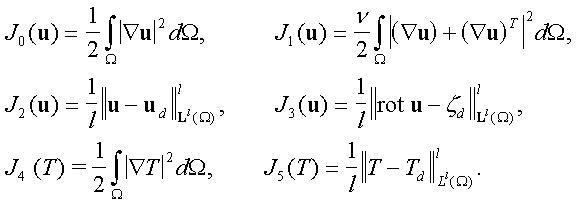 (2)
(2)
Здесь, в частности, функционал ![]() описывает сопротивление в жидкости за счет сил вязкого трения, функционал
описывает сопротивление в жидкости за счет сил вязкого трения, функционал ![]() описывает отклонение завихренности потока rot
описывает отклонение завихренности потока rot
Исследование рассматриваемых экстремальных задач для стационарной системы Обербека-Буссинеска проводится по следующей схеме. Сначала устанавливаются существование слабых решений исходной краевой задачи и доказывается разрешимость задач оптимального граничного управления. Далее
выводится система дифференциальных и граничных соотношений - система оптимальности, связывающая между собой скорость, давление и температуру с сопряженным состоянием x , h , s . Указанная система включает исходную систему дифференциальных уравнений для состояния и сопряженную к ней в определенном смысле систему уравнений вместе с соответствующими граничными условиями для исходного и сопряженного состояний, а также некоторое вариационное неравенство, так называемый принцип минимума, играющий связующую роль между обоими состояниями. При некоторых дополнительных условиях на исходные данные доказывается единственность слабого решения рассматриваемой краевой задачи, так же как и единственность решения соответствующей экстремальной задачи для первого из указанных выше функционалов качества.В частном случае, когда
J=J0 либо J=J4 сопряженная система представляет собой слабую формулировку задачи![]()
![]()
![]() (3)
(3)
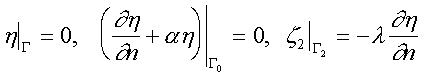
либо
![]()
![]()
![]() (4)
(4)
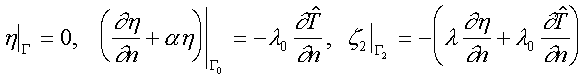
Каждая из систем (3), (4) вместе с исходными уравнениями (1) и принципом минимума, эквивалентным вариационному неравенству
![]()
представляет собой систему оптимальности для рассматриваемой задачи минимизации. Указанная система нелинейна и содержит десять скалярных дифференциальных уравнений, связанных через соответствующие коэффициенты уравнений. Ее теоретическое и численное исследование связано с большими трудностями, тем не менее именно эту систему нужно решать для нахождения искомых граничных управлений
g и g и отвечающих им оптимальных распределений скоростей, давлений и температур в области W . Последнее требует разработки эффективных алгоритмов решения такого типа задач. Системы оптимальности для других функционалов в (2) можно найти в препринте [1].
Литература
[1] Алексеев Г.В. Теоретический анализ стационарных задач граничного управления для уравнений тепловой конвекции // Препринт ИПМ ДВО РАН № 16. Владивосток. Дальнаука. 1996.
[2] Abergel F., Temam R., On some control problems in fluid mechanics // Theoret. Comput. Fluid Mech. 1990. V.1. P.303-325.