ПРОЕКЦИОННО-СЕТОЧНЫЙ МЕТОД РЕШЕНИЯ ЭЛЛИПТИЧЕСКИХ ЗАДАЧ

XVI Международная школа-семинар по численным методам механики вязкой жидкости

НА АДАПТИВНЫХ СЕТКАХ В ОБЛАСТИ С КРИВОЛИНЕЙНОЙ ГРАНИЦЕЙ

В. В. Беляев*, В. П. Шапеев
Институт теоретической и прикладной механики СО РАН,

Новосибирск, Россия

Рассматривается краевая задача для эллиптического уравнения:

a₁₁v_x1x1+ a₁₂v_x1x2 + a₂₂v_x2x2 + b₁v_x1+ b₂v_x2 + cv = f, ,

ℓv| ¶ W = g(x₁,x₂)

в области с криволинейной границей W , ℓ — дифференциальный оператор первого порядка. Область покрывается сеткой с прямоугольными ячейками. При этом возникают регулярные (внутренние) и нерегулярные (граничные) ячейки. Приближенное решение в каждой ячейке ищется в виде полинома второго или третьего порядка. В ячейке выписываются четыре уравнения коллокации и восемь условий согласования или краевых условий. При этом получается переопределенная система линейных уравнений, из которой методом наименьших квадратов находятся коэффициенты полинома. Это связано с тем, что, как правило, применение этого метода позволяет улучшить обусловленность матрицы. В качестве условий согласования решения в соседних ячейках рассматривается непрерывность величины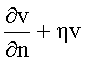 в точках границы ячейки. Здесь n — вектор единичной внешней к границе ячейки нормали, η — параметр метода, зависящий от размера ячейки и влияющий на обусловленность системы линейных уравнений, определяющих приближенное решение.

Эффективность метода проверена как на отдельных уравнениях [1], так и на системах уравнений Стокса и Навье — Стокса [2,3].

Разработанный алгоритм, в отличие от известных, позволяет строить формулы проекционно-сеточного метода решения краевых задач в области с криволинейной границей, содержащей как регулярные, так и нерегулярные ячейки. Классифицированы все типы граничных ячеек, которые возникают при использовании прямоугольной сетки в выпуклой области. Для каждого из них установлен способ нахождения точек, в которых ставятся условия коллокации, согласования или граничные условия. Сохранение прямоугольной сетки внутри области позволяет незначительно увеличивать общее количество вычислений при использовании ячеек различных типов, так как граничными является лишь небольшая часть от общего числа ячеек. Данный метод является альтернативой применению треугольных сеток [1]. Одно из его преимуществ — точная передача границы (не вносится погрешность, связанная с ее аппроксимацией, как это происходит при переносе краевых условий на прямые границы ячеек).

Правильность формул, точность и сходимость метода проверены на решении тестовых задач с различными эллиптическими уравнениями на последовательностях адаптивных сеток, которые сгущаются на основе апостериорной оценки погрешности путем сравнения приближенных решений, полученных в виде полиномов второго и третьего порядков. В качестве тестовой области, содержащей все типы ячеек, использовалась четверть единичного круга. Написана программа, которая формирует адаптивную последовательность сеток, автоматически определяет типы ячеек и находит приближенное решение. На рис. 1 изображена адаптивная сетка, построенная программой при отыскании численного решения задачи, а на рис. 2 — линии уровня точного решения. Видно, что алгоритм, реализованный в программе, “правильно” адаптирует сетку относительно особенности решения.

Рис 1. Адаптивная сетка

Рис 2. Линии уровня (точное решение)

В ходе экспериментов было отмечено значительное влияние расположения точек коллокации, согласования и постановки краевых условий в граничных ячейках на качество аппроксимации. При удачном размещении точек ошибка численного решения в граничных ячейках не превосходит или превосходит незначительно ошибку во внутренней части области, где решение ищется на регулярной сетке. В таблице показана зависимость величины погрешности (модуля разности точного и приближенного решений) от количества ячеек N для равномерной сетки в прямоугольной области (А) и в области с криволинейной границей (В). Анализ результатов показывает, что оба приближенных решения сходятся с одним и тем же порядком, а коэффициенты при остаточных членах различаются незначительно. Это говорит о том, что предложенный здесь способ построения формул метода в нерегулярных граничных ячейках оказался вполне эффективным.

Таблица

N	400	1600	6400	25600
A	3.5·10	4.4·10	6.6·10	3.2·10
B	3.7·10	4.6·10	7.3·10	4.0·10

Работа выполнена при финансовой поддержке РФФИ (код проекта 96–01–01888).

Литература

Слепцов А.Г., Шокин Ю.И. Адаптивный проекционно-сеточный метод для эллиптических задач // Журнал вычислительной математики и математической физики. — 1997. — Т. 37, №5. — С. 572–586.

Сёмин Л.Г., Слепцов А.Г., Шапеев В.П. Метод коллокаций — наименьших квадратов для уравнений Стокса // Вычислительные технологии. — 1996. — Т. 1, №2. — С. 90–98.

Сёмин Л.Г., Шапеев В.П. Метод коллокаций и наименьших квадратов для уравнений Навье — Стокса // Вычислительные технологии. — 1998. — Т. 3, №3. — С. 72–84.