 (1)
(1)XVI Международная школа-семинар по численным методам механики вязкой жидкости
ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ ИНВАРИАНТНЫХ РЕШЕНИЙ РАНГА 1 УРАВНЕНИЙ ДИНАМИКИ ВЯЗКОГО ТЕПЛОПРОВОДНОГО СОВЕРШЕННОГО ГАЗА
В. В. Бублик
Институт теоретической и прикладной механики СО РАН
Новосибирск, Россия
E-mail: bublik@itam.nsc.ru
При разработке и создании новых численных методов и комплексов вычислительных программ для решения задач математической физики важным этапом является тестирование формул, алгоритмов и их программных реализаций на точных решениях. В настоящее время ощущается недостаточность известных точных решений уравнений динамики вязкого теплопроводного газа. Все они, как правило, являются автомодельными. Настоящая работа посвящена построению и исследованию новых тестов для данной модели с помощью методов группового анализа дифференциальных уравнений
[1].Рассматривается система уравнений, описывающая двумерные нестационарные движения вязкого теплопроводного совершенного газа с политропным уравнением состояния:
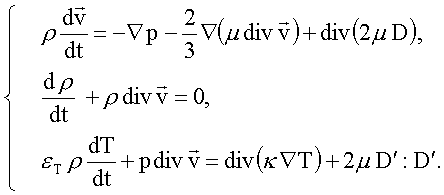 (1)
(1)
Здесь
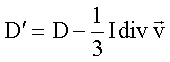 ,
, Групповая классификация уравнений (1) проведена в
[2]. Общее описание всех инвариантных решений ранга 1 для уравнений плоских и осесимметричных движений газа дано в [3, 4]. Всего в указанном классе решений существует 30 типов решений в случае плоской симметрии и 15 типов – в случае осевой. Ранее другими авторами из этих решений описаны только автомодельные в узком смысле слова решения. В данной работе проведен численный анализ поведения остальных решений в зависимости от начальных данных и термодинамических параметров.Инвариантные решения ранга 1 описываются системами обыкновенных дифференциальных уравнений. Для проведения численного анализа поведения решения факторсистемы требуется поставить начальные или краевые условия. В данной работе ограничимся только начальными условиями (т.е. все необходимые начальные данные задаются в одной точке). Для большинства факторсистем, описывающих движения вязкого теплопроводного газа, в начальной точке требуется для трех функций задать значения и первые производные, и для одной – только значение самой функции (при этом подразумевается, что факторсистема не интегрировалась аналитически, даже если одно из уравнений можно проинтегрировать). Таким образом, с учетом начальной точки, решение факторсистемы зависит от восьми параметров. Для качественного исследования поведения решения число этих параметров можно сократить, используя групповые свойства факторсистемы. При этом удобно воспользоваться тем фактом, что факторсистема допускает нормализатор соответствующей подалгебры. Знание нормализатора, конечно, не гарантирует нам полную группу, допускаемую факторсистемой, но даже этого достаточно для сокращения числа существенных параметров в начальной задаче на два-три. Типичная ситуация для плоских движений – положение начальной точки несущественно с групповой точки зрения. В некоторых случаях возможна нормировка ряда величин.
Помимо зависимости поведения от начальных данных необходимо исследование от термодинамических параметров среды. Для системы (1) это три константы: ![]() ,
, ![]() ,
, ![]() . С этим вопросом связано также исследование зависимости от безразмерных констант. При этом не все традиционные безразмерные константы эффективны при этих исследованиях. Например, число Рейнольдса практически непримиримо из-за отсутствия характерного размера (это связано обычно со сложной зависимостью между геометрией обычного потока и геометрией решения в инвариантных переменных). Число Маха обычно дает также мало информации: одной точке решения в пространстве инвариантных переменных обычно соответствует область в пространстве физических переменных, в разных точках которой числа Маха могут существенно отличаться друг от друга (как правило, это связано с нестационарностью движения). Самым подходящим объектом для исследований оказалось число Прандтля
. С этим вопросом связано также исследование зависимости от безразмерных констант. При этом не все традиционные безразмерные константы эффективны при этих исследованиях. Например, число Рейнольдса практически непримиримо из-за отсутствия характерного размера (это связано обычно со сложной зависимостью между геометрией обычного потока и геометрией решения в инвариантных переменных). Число Маха обычно дает также мало информации: одной точке решения в пространстве инвариантных переменных обычно соответствует область в пространстве физических переменных, в разных точках которой числа Маха могут существенно отличаться друг от друга (как правило, это связано с нестационарностью движения). Самым подходящим объектом для исследований оказалось число Прандтля ![]() . В случае системы (1) это число пропорционально величине
. В случае системы (1) это число пропорционально величине ![]() . Удобство его использования заключается в том, что оно зависит только от термодинамических свойств среды и не зависит от геометрии потока. Для ряда решений обнаружено, что при увеличении числа Прандтля область существования физического решения уменьшается.
. Удобство его использования заключается в том, что оно зависит только от термодинамических свойств среды и не зависит от геометрии потока. Для ряда решений обнаружено, что при увеличении числа Прандтля область существования физического решения уменьшается.
Работа поддержана Российским Фондом Фундаментальных Исследований (код проекта 96-01-01888).
Литература