XVI международная школа-семинар по численным методам механики вязкой жидкости
ПОСТРОЕНИЕ И ТЕСТИРОВАНИЕ МЕТОДА КОЛЛОКАЦИЙ И НАИМЕНЬШИХ КВАДРАТОВ РЕШЕНИЯ КРАЕВЫХ
ЗАДАЧ ДЛЯ УРАВНЕНИЙ НАВЬЕ — СТОКСАЛ.Г. Сёмин*, В.П. Шапеев
Институт теоретической и прикладной механики СО РАН
Новосибирск, Россия
E-mail: leon.semin@mailexcite.com
Для численных методов решение краевых задач уравнений Навье — Стокса представляет собой определенные трудности, которые следуют прежде всего из свойств этих уравнений и физики описываемых ими процессов. Многие численные методы, которые хорошо зарекомендовали себя при решении задач для других уравнений, работают плохо при их приложении к уравнениям Навье
— Стокса. В данной работе предлагается сеточный метод коллокаций и наименьших квадратов (КНК) решения краевых задач для уравнений Навье — Стокса. Он является одним из вариантов метода конечных элементов. Метод КНК успешно применялся при решении уравнений в частных производных эллиптического и параболического типов, хорошо зарекомендовал себя при решении эллиптических задач на адаптивных сетках с малым параметром при старшей производной, где могут возникать пограничные и внутренние слои. Поэтому было желательно сформулировать и реализовать его для решения уравнений Навье — Стокса. Для систем уравнений метод впервые применялся нами к решению краевых задач для уравнений Стокса [1].При конечно-элементной аппроксимации краевой задачи для системы уравнений Навье
— Стокса одна из трудностей состоит в правильном учёте уравнения неразрывности
и передаче граничных условий. В предлагаемом здесь методе уравнение неразрывности выполняется точно в каждой ячейке сетки за счёт выбора базиса, легко передаются условия на границах. Для определения коэффициентов разложения решения по базису применяется метод наименьших квадратов, который даёт лучше обусловленную по сравнению с другими методами матрицу результирующей линейной системы.
Рассматривается краевая задача для уравнений Навье — Стокса:
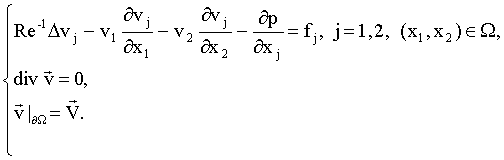
Здесь
Re — число Рейнольдса. Приближённое решение отыскивается в виде кусочно-полиномиальной функции на регулярной сетке для уравнений Озеена: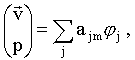
где
— базисные функции, m — номер ячейки. Компоненты вектора скорости представляются в виде полиномов второго порядка, а давление — в виде линейной функции. Коэффициенты 
определяются из уравнений коллокаций и условий согласования или краевых условий. В качестве условий согласования рассматриваются условия непрерывности
выражений
на границе между ячейками [1]. Здесь 
и 
— нормальная и касательная к границе ячейки компоненты скорости, n — вектор единичной внешней нормали к границе рассматриваемой ячейки, 
— некоторый положительный параметр, с помощью которого можно управлять обусловленностью системы уравнений. Получающаяся система алгебраических уравнений имеет вид:
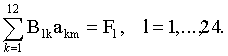
Она переопределена, в ней 24 уравнения и 12 неизвестных. Её решение будем находить по методу наименьших квадратов, а именно, рассмотрим два функционала:
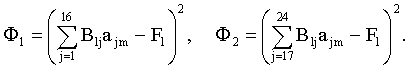
Первый функционал соответствует сумме квадратов невязок уравнений, полученных из условий согласования или краевых условий, второй — сумме квадратов невязок уравнений коллокаций. Решение системы находится из условия минимума этих функционалов. Таким образом, для определения коэффициентов
в каждой ячейке имеем систему уравнений вида:
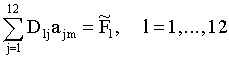
решение которой находим методом прямого исключения.
В качестве одного из тестов рассматривалась задача о течении вязкой несжимаемой жидкости в прямоугольной каверне с движущейся верхней границей. Задача о течении в каверне интересна тем, что она представляет собой модель, на которой можно проверять и сравнивать численные методы. Поэтому ряд исследователей (см. [2] и цитируемую там литературу) проводят на этой задаче сравнение своих результатов. В расчётах по методу КНК хорошо выражены не только главный вихрь, образующийся в каверне, но и вторичные вихри, которые на два порядка слабее главного. Наблюдается хорошее соответствие результатов, полученных в данной работе, с результатами работ, описанных в обзоре [2], а также данными физических экспериментов [3].
На тестах, имеющих точное аналитическое решение, численно показано, что на гладких решениях порядок сходимости метода КНК не хуже второго.
Работа выполнена при финансовой поддержке РФФИ (код проекта 96–01–01888).
Литература