![]() , (1)
, (1)
![]() , (2)
, (2)
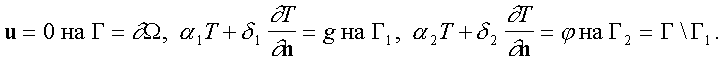 (3)
(3)
XVI Международная школа-семинар по численным методам механики вязкой жидкости
ЗАДАЧИ ОПТИМАЛЬНОГО ГРАНИЧНОГО УПРАВЛЕНИЯ ДЛЯ
СИСТЕМЫ УРАВНЕНИЙ ТЕПЛОВОЙ КОНВЕКЦИИ
Смышляев А.Б., Терешко Д.А.
Институт прикладной математики
Дальневосточного отделения Российской Академии наук
ул. Радио 7, Владивосток, 690041, Россия
В работе рассматриваются задачи оптимального граничного управления для стационарной системы уравнений Обербека-Буссинеска, описывающей установившееся движение вязкой теплопроводной жидкости. На основе [1] развивается эффективный численный алгоритм решения указанных задач. Демонстрируются некоторые результаты вычислительных экспериментов.
В ограниченной области W пространства R2 рассматривается краевая задача для стационарных уравнений Обербека-Буссинеска, имеющая вид
![]() , (1)
, (1)
![]() , (2)
, (2)
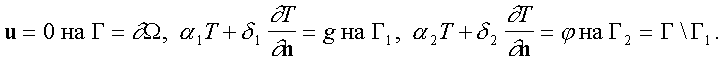 (3)
(3)
Здесь
q - параметр, принимающий значения 0 или 1, что позволяет рассматривать как линейную так и нелинейную краевую задачу, u, p и T - скорость, давление и температура соответственно, b - температурный коэффициент расширения жидкости, G - вектор ускорения свободного падения, c - коэффициент температуропроводности, f - плотность внешних источников тепла, параметры a 1, a 2 и d 1, d 2 в (3) равны либо 0, либо 1 независимо друг от друга, g имеет смысл граничного управления, j - заданная функция, n - единичный вектор внешней нормали (более подробные сведения см. в [2]).Рассмотрим два функционала следующего вида:
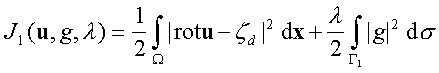 , (4)
, (4)
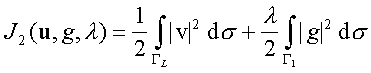 . (5)
. (5)
Здесь вектор
u=(u,v) вместе с соответствующими функциями p и T является решением задачи (1)-(3), z dО L2(W ) - заданная функция, l О [0,1] - заданное число, G LО W - заданный отрезок. С физической точки зрения функционал (4) имеет смысл отклонения по норме L2(W ) функции rotu от заданной функции z d, а равенство нулю или близкое к нему значение функционала (5) означает, что G L является линией раздела течения в W , либо что линия раздела близка к заданной линии G L соответственно.Полученные авторами теоретические результаты позволяют сделать вывод о существовании, а при некоторых дополнительных условиях на исходные данные - и единственности решений задач оптимального граничного управления вида
![]() . (6)
. (6)
При этом предполагается, что управление
g изменяется на выпуклом замкнутом множестве подходящего функционального пространства, а скорость u вместе с (p,T) является слабым решением задачи (1)-(3).При проведении вычислительных экспериментов предполагалось, что
W = {(x,y)О R2: 0 Ј x, y Ј 1}, параметр q = 0 и в уравнении (2) f=0. В соотношениях (1)-(3) был сделан переход от переменных (u,p,T) к переменным (y ,z ,,T) с последующим обезразмериванием. Здесь y - функция тока, z - завихренность.Приближенное решение задач (6) отыскивалось в виде
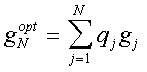 , (7)
, (7)
где
N і 1 - целое число, qj, j=1,...,N - неизвестные вещественные коэффициенты, gj = sin(p jx), j=1,...,N. Из [1] следует для случая, когда q = 0, что решение задач минимизации (6) сводится к решению системы линейных уравнений относительно неизвестных qj, j=1,...,N. Матрица и правая часть последней строятся при помощи решений краевой задачи (1)-(3), где в первом соотношении формулы (3) полагается g = gj, j=1,2,...,N.На основании полученных результатов вычислительных экспериментов можно сделать следующие выводы: 1) в рамках модели (1)-(3) при
q = 0 не удается получить равнозавихренного течения в области W за счет выбора температуры на границе, хотя это можно сделать, например, за счет выбора первой компоненты вектора скорости (см. [1]). 2) Однако, за счет надлежащего выбора температуры на части границы области W значение функционала (5) можно сделать достаточно малым, что физически означает возможность разделения течения так, как это указано на рис. 1.Литература
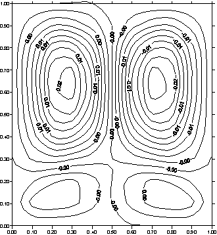
Рис. 1.
Пояснения к рисунку 1. На рисунке изображены линии уровня функции тока, полученной при решении задачи (6) (при
k=2). В соотношениях (3) предполагается, что a 1 = a 2 = 1, а d 1 = d 2 = 0, функция j во втором соотношении формулы (3) равна 1 на верхней стенке (при y=1) области W и 0 - на левой и правой стенках (при x=0 и x=1).