Детерминированный хаос и его редукция в микроэволюционной модели Риккера-Мэя1

Шаповалов А.В., Евдокимов Е.В.
Томский государственный университет

Аннотация:

Численными и аналитическими методами исследованы особенности динамики микроэволюционной модели Риккера-Мэя. Показано, что отбор в данной системе всегда направлен в сторону увеличения средней приспособленности в популяции, что соответствует основной теореме естественного отбора Фишера для моделей популяций с непрерывным временем. При наличии в популяции разнообразия по мальтузианскому и ресурсному параметрам течение отбора сопровождается последовательной сменой динамических режимов от стационарного состояния через предельные циклы к хаосу и наоборот - в зависимости от направления отбора. Приведены интегралы движения системы, которые позволяют ввести простые парные комбинации популяционных переменных, линейно зависящих от времени. Многомерная хаотическая динамика популяции в целом редуцируется к одномерной хаотической динамике.

Micro-evolution dynamics is studied both analytically and numerically in the framework of the Ricker-May model. The selection is shown to be tended to extension of mean value of population fitness that corresponds to the Fisher's theorem on natural selection in population models with continuous time. The selection in population with a non-zero value of variance in Malthusian and resource parameters is accompanied by successive change of dynamic regimes from a stationary state through limit cycles to chaos and inversely in dependence upon the selection tend. Integrals of motion are presented that results in pairwise combinations of population variables linearly dependent on time. Multidimensional chaotic population dynamics is reduced to a one-dimensional chaotic dynamics.

Ключевые слова: динамика микроэволюционной модели, отбор

Микроэволюционная модель Риккера-Мэя описывает динамику плотностно-зависимого отбора в биологических популяциях с бесполым размножением и неперекрывающимися поколениями и имеет следующий вид [1]:

\begin{displaymath} x_{n+1}^i=x_{n}^i\exp[R^i(1-\sum_j x_{n}^j/K^i)].\eqno (1) \end{displaymath}

Здесь $x^i_n$ и $x^i_{n+1}$ - численности особей $i$-го генотипа в $n$-ый и $(n+1)$-ый сезоны размножения, $R^i$ и $K^i$ - соответствующие данному генотипу значения мальтузианского и ресурсного параметров, $j$ меняется от $1$ до $L$, где $L$ - число различных генотипов в популяции. Для данной модели показано, что в зависимости от значений управляющих параметров $R^i$ и $K^i$ она демонстрирует различные типы динамических режимов: монотонное стремление к стационарному состоянию, предельные циклы и детерминированный хаос [1]; [2].

В работе численными и аналитическими методами исследовались особенности динамики данной системы в случаях, когда в популяции задано такое разнообразие по значениям управляющих параметров, чтобы часть из них находилась в монотонной области, часть - в области предельных циклов, часть - в области хаоса, при этом начальные численности особей разных генотипов существенно отличались.

Рис. 1. Смена динамических режимов в ходе отбора.
\begin{figure} \begin{center} \epsfxsize=6.5in %%\epsfysize=12cm \epsfbox{fig1.eps} \end{center} \end{figure}

Показано, что отбор в данной системе всегда направлен в сторону увеличения средней приспособленности в популяции, определяемой как $\langle\exp[R^i(1-\sum_j x_{n}^j/K^i)]\rangle$, что соответствует основной теореме естественного отбора Фишера, известной для моделей популяций с непрерывным временем. Однако нелинейные свойства исследуемой системы вносят определенные особенности в ее эволюционную динамику.

Во-первых, отбор всегда идет в сторону увеличения ресурсного параметра $K$, если в популяциях есть соответствующее генетическое разнообразие. При его отсутствии отбор как таковой в популяции не наблюдается, несмотря на наличие дисперсии по мальтузианскому параметру $R$.

Во-вторых, в отсутствие дисперсии по $K$ и при наличии разнообразия по $R$ в популяции наблюдается сосуществование всех генотипов. Их равновесное распределение устанавливается в течение первых трех-четырех поколений и далее не меняется.

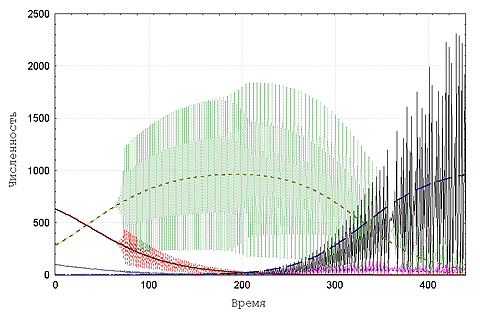
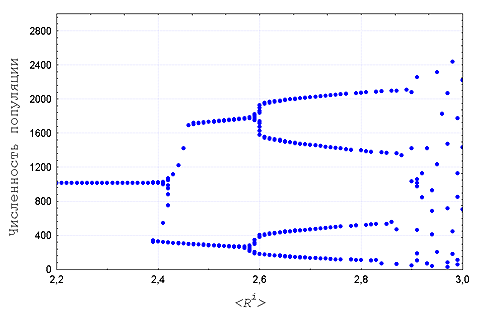
В-третьих, при наличии в популяции разнообразия по мальтузианскому и ресурсному параметрам течение отбора сопровождается последовательной сменой динамических режимов от стационарного состояния через предельные циклы к хаосу и наоборот - в зависимости от направления отбора по $K$ (Рис. 1). В популяции наблюдается последовательная замена одного доминирующего генотипа другим, а тип наблюдаемого при этом динамического режима определяется среднепопуляционным значением мальтузианского параметра (Рис. 2).

Рис. 2. Изменение численностей особей с различными генотипами в ходе отбора. Тонкие линии - отображение Риккера-Мэя, толстые линии - модель Вольтерра- Лотки.
\begin{figure} \begin{center} \epsfxsize=6.5in %%\epsfysize=12cm \epsfbox{fig2.eps} \end{center} \end{figure}

Диаграмма $\{\sum_j x^j_n, \langle R^j \rangle_n\}$ носит явный бифуркационный характер, типичный для популяций, описываемых одномерным отображением Риккера, роль управляющего параметра в которой играет среднепопуляционное значение $\langle R^j \rangle_n\}$ (Рис. 3).

Рис. 3. Взаимосвязь между среднепопуляционным значением мальтузианского параметра $\langle R^j \rangle _n$ и численностью популяции в ходе отбора. Для построения диаграммы в каждом поколении рассчитывали $\langle R^j \rangle _n$ и откладывали против него соответствующее значение суммарной численности популяции.
\begin{figure} \begin{center} \epsfxsize=6.5in %%\epsfysize=12cm \epsfbox{fig3.eps} \end{center} \end{figure}

Подобные результаты для однолокусной двухаллельной модели популяции с половым размножением были получены Е. Фрисманом [3].

Конкуренция между особями различных генотипов, представленная в рассматриваемой модели выражением $1-\sum_j x^j_n/K^i$, определяет коллективный тип поведения в системе. Это позволяет ввести простые парные комбинации популяционных переменных

\begin{displaymath} z_{n}^i=\displaystyle\frac{K^i}{R^i}\log x_{n}^i - \displaystyle\frac{K^L}{R^L}\log x_{n}^L,\eqno (2) \end{displaymath}

линейно зависящих от дискретного времени $n$,
\begin{displaymath} z_{n}^i=z_{0}^i+(K^i-K^L)n.\eqno (3) \end{displaymath}

Тем самым многомерная хаотическая динамика популяции в целом редуцируется к одномерной хаотической динамике по переменной $x^L$. Введение переменных (3) обусловлено наличием интегралов движения
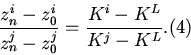
\begin{displaymath} \displaystyle\frac{z_{n}^i-z_{0}^i}{z_{n}^j-z_{0}^j}= \displaystyle\frac{K^i-K^L}{K^j-K^L}.\eqno (4) \end{displaymath}

Отображение Риккера-Мэя (1) можно рассматривать как интегральную форму

\begin{displaymath} x^i(t+\delta t)=x^i(t) \exp \left [ R^i\int_t^{t+\delta t}... ...\displaystyle\frac{\sum_j x^j(\xi)}{K^i}\right )d\xi \right] \end{displaymath}

логистической модели Вольтерра-Лотки
\begin{displaymath} \dot x^i=x^iR^i\left (1-\displaystyle\frac{\sum_j x^j}{K^i}\right) \eqno (5) \end{displaymath}

на малом временном интервале $\delta t$. Сравним динамику отбора в популяциях, описываемых отображением Риккера-Мэя (1) и моделью Вольтерра-Лотки (5) при одинаковых значениях параметров и начальных данных. Результаты представлены на Как видно, численные решения системы Вольтерра-Лотки совпадают с текущими средними для популяционных переменных системы Риккера-Мэя при всех режимах, в том числе и в хаотической области. Совпадают также указанные выше интегралы движения (4) и линейно зависящие от времени парные комбинации переменных (2). Следовательно, пространство популяционных переменных для этих систем можно представить в виде произведения $(L-1)$-мерного и одномерного подпространств, в первом из которых динамика обеих систем совпадает и является регулярной, а во втором - в дискретном случае она имеет сложный характер, в том числе и хаотический, в непрерывном случае - она регулярна.

Литература

1
May R.M. Biological populations with non-overlapping generations: stable points, stable cycles and chaos.// Science, 186, 1974, 645-647.

2
Hassel M.P., Comins H.N., May R. Spatial structure and chaos in insect population dynamics.// Nature, 353, 1991, 255-258.

3
Фрисман Е.Я. Эволюция характера динамики численности популяции: переход к хаосу. // В сб. Исследования по математической биологии. Ред. Э.Э.Шноль. Пущинский НЦ РАН, Пущино, 1996, 75-87.
1
Работа поддержана грантами Минобразавания РФ Е00-12.0-239 и Е00- 1.0-126.
Ваши комментарии
[SBRAS]
[Головная страница]
[Конференции]
[СО РАН]

© 2001, Сибирское отделение Российской академии наук, Новосибирск
© 2001, Объединенный институт информатики СО РАН, Новосибирск
© 2001, Институт вычислительных технологий СО РАН, Новосибирск
© 2001, Институт систем информатики СО РАН, Новосибирск
© 2001, Институт математики СО РАН, Новосибирск
© 2001, Институт цитологии и генетики СО РАН, Новосибирск
© 2001, Институт вычислительной математики и математической геофизики СО РАН, Новосибирск
© 2001, Новосибирский государственный университет
Дата последней модификации Sunday, 07-Oct-2001 14:32:48 NOVST