§ 1.1. Сведения из теории обыкновенных дифференциальных уравнений. Постановки задач

В этом параграфе кратко напоминаются основные сведения из теории обыкновенных дифференциальных уравнений, описываются возможные методы приближенного решения задачи Коши и постановка задачи о разностных методах решения задачи Коши.

1.1.1. Воспоминания о курсе "Обыкновенные дифференциальные уравнения"

Если не оговорено противное, мы будем рассматривать систему обыкновенных дифференциальных уравнений первого порядка, разрешенных относительно старшей производной, т. е. систему вида

x′ = f(t, x),

(E)

где f: R×R^m → R^m — непрерывная функция.

На протяжении всего курса R^m — m-мерное линейное вещественное пространство. Мы всегда считаем, что в R^m фиксирован базис и отождествляем R^m с координатным m-мерным вещественным пространством: точки из R^m — это упорядоченные наборы m вещественных чисел x = (x₁, ..., x_m). Таким образом, (E) — это сокращенная форма записи системы дифференциальных уравнений

x′1= f1(t, x1, ..., xm),

...

x′m= fm(t, x1, ..., xm),

в которой x = (x₁, ..., x_m), а f(t, x) = (f₁(t, x), ..., f_m(t, x)) = (f₁(t, x₁, ..., x_m), ..., f_m(t, x₁, ..., x_m)). Кроме того, предполагается, что в R^m фиксирована некоторая норма || · ||.

Решением уравнения (E) на промежутке [a, b] называется функция φ: [a, b] → R^m, обращающая (E) в тождество на [a, b]:

φ′(t) ≡ f(t, φ(t)),   t ∈ [a, b].

График решения (лежащий, по определению, в расширенном фазовом пространстве R×R^m) называется интегральной кривой I_φ. Проекция интегральной кривой на фазовое пространство R^m параллельно R называется траекторией T_φ. Здесь же отметим, что независимую переменную t мы в первой главе всегда будем трактовать как время.

В общей ситуации, уравнение (E) имеет бесконечное множество решений (точнее, m-параметрическое семейство решений). Для того чтобы выделить одно из них, нужны дополнительные условия (уравнения). Такие условия могут быть различными. В этой главе рассматривается только один вид дополнительных условий, так называемые начальные условия — требование, чтобы решение в заданной точке принимало заданное значение:

x(t0) = x0.

(C)

Задача о нахождении решения уравнения (E), удовлетворяющего начальному условию (C), называется задачей Коши. Обозначение "задача Коши (E) – (C)" будет универсальным, т.е. действовать на протяжении всей книги; универсальные обозначения и предположения будут заключаться в рамку:

Задача Коши (E) – (C).

Говорят, что функция f удовлетворяет условию Липшица по второму аргументу, если

∃(L) ∀(t ∈ R; x, y ∈ Rm) [||f(t, x) – f(t, y)|| ≤ L||x – y||]

(число L называется константой Липшица).

Фундаментальное в теории обыкновенных дифференциальных уравнений утверждение о разрешимости задачи Коши — следующая

Теорема Коши — Пикара. Если функция f непрерывна по первому аргументу и удовлетворяет условию Липшица по второму, то задача Коши (E) – (C) на любом отрезке вида [t₀, t₀ + T] имеет единственное решение.

Всюду ниже мы всегда будем предполагать, что

выполнены условия теоремы Коши — Пикара. При этом обозначение L для константы Липшица будет универсальным.

Простым достаточным условием выполнения условия Липшица является следующее утверждение. Если функция f дифференцируема по второму аргументу и ее производная равномерно ограничена некоторой константой L: ||∂f(t, x)/∂x|| ≤ L при всех (t, x) ∈ R×R^m, то она удовлетворяет условию Липшица с константой L.

Это же утверждение в "координатной форме": если функции (t, x) → f_i(t, x) = f_i(t, x₁, ..., x_m) дифференцируемы по последним m аргументам и все частные производные ограничены некоторой константой K: |∂f_i(t, x₁, ..., x_m)/∂x_j| ≤ K при всех (t, x₁, ..., x_m) ∈ R×R^m и i, j = 1, ..., m, то функция f удовлетворяет условию Липшица с некоторой константой L. (Найдите L через K и m.)

Несколько слов о геометрической трактовке уравнения (E). В каждой точке расширенного фазового пространства это уравнение задает направление касательной к интегральной кривой, поскольку предписывает, чему должна равняться производная φ′(t) в точке (t, x) = (t, φ(t)). Если в каждой точке R×R^m вектором (1, f(t, x)) указать направление касательной, то получившийся объект называют полем направлений, отвечающим уравнению (E)

Рис. 1.

(рис. 1, а). Интегральная кривая должна "касаться" векторного поля в каждой своей точке (рис. 1, б). Поэтому расширенное фазовое пространство можно представлять как парк, часто заполненный стрелками-указателями, а решение — как прогулку по этому парку в соответствии со стрелками (в направлении, указываемом стрелками).

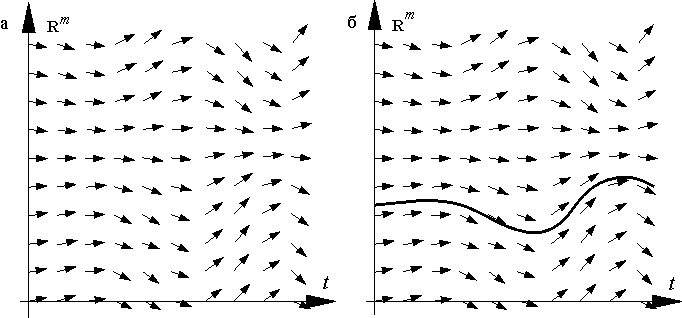
Утверждение о гладкости решений. Если в задаче (E) – (C) функция f является k раз непрерывно дифференцируемой, то ее решение φ непрерывно дифференцируемо k + 1 раз.

1.1.2. Для чего нужны дифференциальные уравнения и чего мы от них хотим?

Дифференциальные уравнения являются инструментом познания мира и, как всякий инструмент, они развиваются и самосовершенствуются. Поэтому с точки зрения теории это самодостаточный объект. С прикладной же точки зрения дифференциальные уравнения описывают окружающий нас мир, и с их помощью мы можем узнавать о нем новое. "Познание мира" с помощью дифференциальных уравнений обычно состоит из двух этапов: составление модели (дифференциального уравнения, описывающего то или иное явление) и исследование получившейся модели.

Нас интересует в данном курсе второй этап. Поскольку именно решения описывают те или иные природные процессы, в конечном счете прикладнику важна информация именно о них. Большáя часть теории обыкновенных дифференциальных уравнений посвящена изучению решений в случаях, когда оно точно не известно. Это так называемая качественная теория обыкновенных дифференциальных уравнений. К ней относится, например, теория устойчивости, позволяющая, не зная решения, по свойствам уравнения указать свойства устойчивости решений. В конкретных задачах часто возникает необходимость найти решение или иметь возможность вычислить решение в каждой точке. Иногда решение некоторых дифференциальных уравнений удается выписать в явном виде. В то же время множество дифференциальных уравнений, решения которых можно в явном виде выразить через элементарные функции, весьма и весьма бедное. Уже простейшее нелинейное уравнение первого порядка x′ = t² + x² не допускает решений в квадратурах. Поэтому нужны методы, позволяющие вычислять решения произвольных дифференциальных уравнений приближенно.

1.1.3. Как можно решать дифференциальные уравнения приближенно? Метод разложения в ряды.

Исторически первым методом решения дифференциальных уравнений, который использовал еще их автор Ньютон, был метод разложения в ряды. Искомое решение разлагается в ряд (например, Тейлора) с неизвестными коэффициентами. Этот ряд подставляется в (E) и из получившегося уравнения находятся коэффициенты.

Предположим, например, что в уравнении (E) функция f аналитична, т.е. допускает разложение в ряд по степеням t и x:

f(t, x) = f00 + f10t + f01x + f20t2 + f11tx+ f02x2 + ... .

(1)

Тогда известно (это достаточно громоздко доказываемая теорема), что решение φ задачи (E) – (C) также аналитично, т.е. представимо в виде ряда

φ(t) = x0 + x1t + x2t2 + ...

(2)

с неизвестными пока коэффициентами x₀, x₁, .... Очевидно,

φ′(t) = x1 + 2x2t + 3x3t2 + ... .

(2)

Подставим разложения (1) – (3) в уравнение (E) и в получившемся уравнении приравняем коэффициенты при одинаковых степенях t. Кроме того, подставим разложение (2) в начальное условие (для простоты, будем считать, что t₀ = 0). Получим бесконечную систему уравнений

x0 = x0, x1 = f00 + f01x0 + f02x20+ ..., 2x2 = f10 + f01x1 + f11x0 + 2f02x0x1 + ..., 3x3 = f20 + f11x1 + f01x2 + f02x21+ 2f02x0x1 + ..., . . .

Из второго уравнения находится x₁ (через x₀ и f_ij), из третьего — x₂ (через x₀, x₁ и f_ij) и т. д. Таким способом могут быть найдены все коэффициенты в разложении (2). Частичные суммы ряда (2) аппроксимируют решение с заданной точностью.

Задача 1.1.1. Найдите описанным методом решение скалярной задачи Коши x′ = ax, x(t₀) = x⁰.

Эти методы требуют, как правило, большого объема аналитической плохо алгоритмизируемой работы. Например, для нахождения коэффициентов ряда Тейлора решения нужно вычислять производные высоких порядков от правой части уравнения. В силу этого разложения решений в такие ряды пока мало пригодны для практического использования на ЭВМ. Кроме того, эти методы обладают плохими свойствами устойчивости в вычислительном плане.

1.1.4. Как можно решать дифференциальные уравнения приближенно? Метод последовательных приближений.

Для отыскания приближенного решения можно воспользоваться также методом последовательных приближений. Напомним его суть. Задача Коши (E) – (C) эквивалентна интегральному уравнению

x(t) = x0 + ∫ t t0 f[s, x(s)]ds,   t ∈ [t0, t0 + T]

(4)

в следующем смысле: если φ — решение задачи Коши (E) – (C), то φ удовлетворяет уравнению (4) и наоборот.

Обозначим правую часть уравнения (4) через (Jx)(t). Тогда оно перепишется в операторном виде

x = Jx.

Если применить к получившемуся уравнению метод простой итерации, начиная, например, с функции x⁰(t) ≡ x⁰, то получим рекуррентно определяемую последовательность функций:

xn(t) = Jxn–1 = x0 + ∫ t t0 f[s, xn–1(s)]ds,    n = 1, 2, ... .

(5)

Известно, что последовательность функций xⁿ равномерно сходится к решению задачи (E) – (C), причем известна оценка скорости сходимости. Если теперь заменить в (5) интеграл (вовсе не обязательно берущийся) какой-либо квадратурной формулой (возможность такой замены требует, конечно, обоснования), то получится метод, позволяющий вычислять все более и более точные приближения решения.

Задача 1.1.2. Найдите описанным методом решение скалярной задачи Коши x′ = ax, x(t₀) = x⁰.

Поскольку этот метод требует большого объема вычислительной работы (на каждой итерации приходится неоднократно вычислять значения правой части уравнения), он играет, в основном, теоретическую роль - например, он полезен при доказательстве теоремы Коши — Пикара или при доказательстве утверждений о дифференцируемости решений по параметру или начальным данным.

1.1.5. Как можно решать дифференциальные уравнения приближенно? Асимптотические методы.

Искать приближенные решения можно также, пытаясь найти интегрируемое в квадратурах дифференциальное уравнение, решения которого аппроксимируют решения исходного. Такое уравнение указать, как правило, все-таки трудно. Поэтому можно попытаться искать более простое уравнение, аппроксимирующее решения исходного. С этим направлением тесно связаны асимптотические методы или методы разложения по параметру. В данном курсе мы их тоже не рассматриваем.

В настоящее время наиболее универсальными и эффективными методами приближенного решения дифференциальных уравнений признаны так называемые конечно-разностные (их еще называют разностными или сеточными) методы.

1.1.6. Конечно-разностные методы. Постановка задачи.

Пусть для любого τ > 0 задано множество G_τ точек t₀ < t₁ < ... < t_n = t₀ + T отрезка [t₀, t₀ + T] такое, что τ = max_{0≤i≤ n}{t_i+1 – t_i}. Множество G_τ называется сеткой, его элементы — узлами, а числа τ_i = t_i+1 – t_i — шагами сетки. Если τ_i ≡ τ = T/n, то говорят о сетке с постоянным шагом, или сетке с шагом τ, или равномерной сетке.

Конечно-разностным или разностным методом приближенного решения задачи (E) – (C) называют любые методы (приемы, способы), позволяющие для каждого τ > 0 указать φτ: Gτ → Rm (такие функции называют сеточными), которая в том или ином смысле аппроксимирует решение φ задачи (E) – (C). Разумеется, возникает вопрос: в каком смысле понимать фразу "сеточная функция аппроксимирует решение"? Поскольку φτ и φ принадлежат разным пространствам, то естественно изометрично вложить пространство сеточных решений и пространство решений в одно пространство, и уже в этом пространстве измерять расстояние между ними. Например, вложить пространство сеточных функций в пространство непрерывных функций, заменив сеточную функцию φτ ломаной φτ, и считать, что φτ хорошо аппроксимирует φ, если ||φτ – φ||C ≝ max{||φτ(t) – φ(t)||Rm: t ∈ [t0, t0 + T]} мала.

Чаще поступают следующим образом. "Проектируют" решение φ на пространство сеточных функций S_τ, ставя в соответствие функции φ ее сужение P_τφ на сетку G_τ. На пространстве сеточных функций S_τ задают норму, обычно, либо равномерную: ||y|| = max_t∈Gτ{|| y(t)||}, либо вадратичную: ||y|| = (∑_t∈Gτ || y(t)||²)^1/2. Теперь можно считать, что φ_τ хорошо аппроксимирует φ, если ||φ_τ –P_τφ||_Sτ мала.

Всюду ниже мы будем считать, что на пространстве Sτ задана равномерная норма и будем обозначать эту норму через || · ||τ.

Если x — сеточная функция на Gτ, то ее значение в точке ti мы всегда будем обозначать через xi, а не стандартно x(ti).

Pτφ для любой функции φ на отрезке [t0, t0 + T] всегда обозначает сужение φ функции на сетку Gτ: [Pτφ]i = [Pτφ](ti) = φ(ti).

File based on translation from T_EX by T_TH, version 3.05.
Created 23 May 2002, 19: 09.