§ 1.2 Разностные схемы. Сходимость, аппроксимация, устойчивость

В данном параграфе на примере явного метода Эйлера даются основные понятия теории разностных схем — понятия сходимости, аппроксимации и устойчивости. Доказывается теорема Лакса. Описываются основные приемы построения разностных схем.

1.2.1. Метод ломаных Эйлера.

Напомним, что метод ломаных Эйлера – это метод нахождения аппроксимирующей интегральную кривую ломаной, который в образах парка со стрелками-указателями может быть представлен так (рис. 2). Из точки (t₀, x₀) = (t₀, x⁰) расширенного фазового пространства движемся τ "секунд", сообразуясь со стрелкой, помещенной в этой точке, и не обращая внимания на остальные стрелки. Придя (через время τ) в точку (t₁, x₁), меняем направление, пользуясь указанием, задаваемым стрелкой в точке (t₁, x₁); через τ секунд приходим в точку (t₂, x₂), опять меняем направление и  т. д. Полученная траектория и является ломаной Эйлера, аппроксимирующей решение задачи (E) – (C).

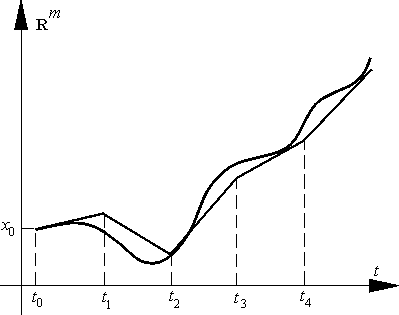
Рис. 2.

Легко видеть, что координаты i-й вершины (i = 1,..., n) ломаной Эйлера определяются формулами

ti = t0 + iτ,   x0 = x0,    xi = xi–1 + τf(ti–1, xi–1).

(1)

Перепишем эти равенства в следующем виде:

xi – xi–1 τ  – f(ti–1, xi–1) = 0,  если i = 1,..., n,

xi = x0, если i = 0.

1.2.2. Операторная запись задачи (E) – (C).

Запишем метод ломаных Эйлера в общем виде, в котором могут быть записаны другие разностные методы и который позволяет укладывать исследование таких методов в общую схему. Для этого сначала запишем задачу (E) – (C) в операторной форме. Начальное условие (C) можно записать в виде

g(x) = 0,

где функция g имеет вид g(x) = x(t₀) – x⁰. Тогда начальную задачу (E) – (C) можно записать в операторной форме

F(x) = 0,

(O)

где F(x) = (x′(·) – f(·, x), g(x)). Не будем обсуждать подробно вопрос об областях определения и значений оператора F. В случае задачи (E) – (C) можно считать, например, что областью определения D(F) оператора F служит пространство C¹([t₀, t₀ + T], R^m) непрерывно дифференцируемых на отрезке [t₀, t₀ + T] функций со значениями в R^m, а областью значений R(F) — декартово произведение C¹([t₀, t₀ + T], R^m)×R^m. Заметим, что решение φ задачи (E) – (C) есть прообраз нуля для оператора F: φ = F^–1(0).

1.2.3. Операторная форма метода ломаных Эйлера.

Пусть x — сеточная функция из S_τ. Определим на S_τ оператор F_τ равенством

[Fτ(x)]i = { xi – xi–1 τ   –  f(ti–1, xi–1),  если i = 1, ..., n, xi – x0,  если i = 0;

(2)

(Здесь [F_τ(x)]_i обозначает значение сеточной функции [F_τ(x)] в точке t_i.)

Задача о нахождении ломаной Эйлера, очевидно, эквивалентна задаче о нахождении решения φ_τ уравнения

Fτ(x) = 0

(S)

в пространстве Sτ сеточных функций в следующем смысле: значения (φτ)i решения уравнения (S) в узлах сетки и только они являются ординатами вершин ломаной Эйлера в точках ti (см. формулу (1)). Таким образом, вместо точного решения φ = F–1(0) мы ищем приближенное решение φτ = Fτ–1(0).

1.2.4. Разностные схемы.

Любое уравнение вида (S) для нахождения сеточной функции x будем называть разностной схемой, а его (уравнения) решение, которое мы всегда будем обозначать φ_τ, — разностным или сеточным решением (уравнения (S)). Оператор F_τ будем называть разностным оператором. Разумеется, в таком общем виде определение разностной схемы никак не связано с исходной задачей Коши (E) – (C) (уравнением (O)). В то же время, если в (S) оператор F_τ определен формулой (2), то разностная схема (S) имеет к задаче (E) – (C) самое непосредственное отношение (объяснить, что означают эти слова, и есть цель остальной части параграфа).

В последнем случае разностная схема (S) называется явной (разностной) схемой Эйлера. Явной она называется потому, что ее решение может быть выписано в явном виде с помощью рекуррентных соотношений:

(φτ)0 = x0,

(φτ)i = (φτ)i–1 +τf[ti–1,(φτ)i–1],   i = 1, ..., n.

Единственное отличие метода ломаных Эйлера от явной схемы Эйлера заключается в том, что в первом ищется функция, заданная на отрезке [t₀, t₀ + T] (ломаная Эйлера), а во втором — на сетке G_τ (вершины этой ломаной).

Задача 1.2.1. Докажите, что разностное решение φ_τ явной схемы Эйлера для задачи Коши

x′ = ax,   x(t0) = x0

(a ∈ R) на равномерной сетке (τ_i = iτ) задается формулой (φ_τ)_i = x⁰(1 + τa)ⁱ.

1.2.5. Пример. Сходимость явной разностной схемы Эйлера.

В условиях задачи 1.2.1 разностное решение φ_τ аппроксимирует решение φ(t) = x⁰e^at интересующей нас исходной (дифференциальной) задачи в следующем смысле: при всех t ∈ [0, T]

(φτ)i→ x0eat при τ→ 0,

(3)

где i = [t/τ] (здесь [t/τ] — целая часть числа t/τ; ниже мы наряду с обозначением [a] для целой части числа a используем обозначение {a} для его дробной части: a = [a]+ {a}). Действительно,

lim τ→0 (φτ)i =  lim τ→0 x0(1 + τa)i = x0· lim τ→0 (1 + τa)[t/τ] =

= x0· lim τ→0 (1 + τa)t/τ–{t/τ} =

= x0· lim τ→0 (1 + τa)t/τ· lim τ→0 (1 + τa)–{t/τ}.

Сомножитель lim_τ→0(1 + τa)^–{t/τ} равен единице, поскольку {t/τ} ∈ (0, 1). Второй сомножитель также вычисляется тривиально:

lim τ→0 (1 + τa)t/τ =  lim τ→0 (1 + τa)[1/(τa)] ·at =  [ lim τ→0 (1 + τa)1/τa ] at  = eat

и соотношение (3) доказано.

Задача 1.2.2. Докажите более сильное, чем (3) утверждение

||φτ – Pτφ||τ→ 0 при τ→ 0.

означающее, что предельное соотношение (3) выполнено равномерно по i ∈ {1, ..., n).

1.2.6. Сходимость разностных схем.

Будем говорить, что разностная схема (S) сходится (к решению φ задачи (E) – (C)), если

||φτ – Pτφ||τ→ 0 при τ→ 0.

(4)

Сходимость разностной схемы означает, что при достаточно малом τ значения сеточного (приближенного) решения φ_τ и точного решения φ мало отличаются. Соотношение (4) на практике оказывается мало полезным, поскольку на основании его нельзя судить о том насколько малым мы должны выбрать шаг τ, чтобы в узлах сетки точное и приближенное решения отличались друг от друга не более, чем на ε (заранее заданную точность). Если удается доказать, что при достаточно малых τ > 0

||φτ – Pτφ||τ ≤ Cτk,

(5)

где C — не зависящая от τ константа, то говорят, что схема (S) сходится с порядком k (или является схемой k-го порядка (сходимости)). Оценка (5), если в ней известна (для конкретной задачи (E) – (C)) константа C, позволяет по заранее выбранной точности ε a priori выбрать шаг так, чтобы приближенное решение аппроксимировало решение данной (дифференциальной) задачи Коши с точностью ε:

||φτ – Pτφ|| τ ≤ ε;

достаточно взять τ ≤ k√ε/C.

1.2.7 Аппроксимация.

Явная схема Эйлера обладает двумя важными свойствами, из которых, как будет показано ниже, последует ее сходимость с первым порядком. Во-первых, при достаточно малых τ

||Fτ(Pτφ)||τ ≤ Caτ,

(6)

где C_a — константа, не зависящая от τ, а φ — как обычно, точное решение задачи (E) – (C). В этом случае говорят, что схема (S) имеет первый порядок аппроксимации на решении. (Если в правой части неравенства (6) стоит C_aτ^k, то, соответственно, говорят о схеме k-го порядка аппроксимации (на решении).) Другими словами, неравенство (6) эквивалентно тому, что ||F_τ(P_τφ)||_τ = O(τ) (в случае схемы k-го порядка аппроксимации — O(τ^k)). Тот факт, что разностная схема обладает аппроксимацией на решении, означает, грубо говоря, что при подстановке точного решения дифференциальной задачи в разностную схему мы получаем невязку соответствующего порядка малости по τ. (Было бы идеально, если бы после такой подстановки мы получали в левой части нуль, однако в общем случае конструктивно такие схемы выписать нельзя.)

Часто вместо свойства аппроксимации на решении рассматривают формально более жесткое требование, которое называют свойством аппроксимации (в зарубежной литературе — согласованностью); именно, говорят, что схема (S) является схемой k-го порядка аппроксимации на функции x, если при достаточно малых τ

||Fτ(Pτx) – PτF(x)||τ ≤ Caτk.

Обычно требуется, чтобы схема обладала свойством аппроксимации на множестве функций из некоторого класса гладкости. Очевидно, если решения дифференциального уравнения (E) m раз непрерывно дифференцируемы, а разностная схема обладает k-м порядком аппроксимации (согласованности) на m раз непрерывно дифференцируемых функциях, то она обладает k-м порядком аппроксимации на решении.

1.2.8. Аппроксимация явной схемы Эйлера.

Покажем, что если функция f в (E) непрерывно дифференцируема по t и x, то явная схема Эйлера имеет первый порядок аппроксимации на решении. Действительно, пусть φ — решение задачи (E) – (C):

φ′(t) ≡ f[t, φ(t)],   t ∈ [t0, t0 + T].

Поскольку f дифференцируема по t и x, решение φ дважды непрерывно дифференцируемо (см. утверждение о гладкости решений). В частности, найдется M такое, что ||φ′′(t)|| ≤ M при всех t ∈ [t₀, t₀ + T]. Кроме того, в силу гладкости φ для любых t = 1, ..., n

φ(ti) = φ(ti–1 + τ) = φ(ti–1) +τφ′(ti–1) +  τ2 2 φ′′(ti–1 + Φiτ),

где Φ ∈ (0, 1). Но тогда

[Fτ(Pτφ)]i =  (Pτφ)i – (Pτφ)i–1 τ – f[ti–1, (Pτφ)i–1] =

=  φ(ti) – φ(ti–1) φ – f[ti–1, φ(ti–1)] =

=  φ(ti–1) + τφ′(ti–1) +  τ2 2 φ′′(ti–1 + Φiτ) – φ(ti–1) τ  –

– f[ti–1, φ(ti–1)] = φ′(ti–1) +  τ2 2 φ′′(ti–1 + Φiτ) – f[ti–1, φ(ti–1)] =

=  τ 2 φ′′(ti–1 + Φiτ).

(Если i = 0, то очевидно, [F_τ(P_τφ)]_i = 0.) Из сказанного следует, что

||Fτ(Pτφ)|| τ =  max 0≤i≤n ||[Fτ(Pτφ)]i|| ≤

≤  τ 2 max 0≤i≤n ||φ′′(ti–1+Φiτ)|| ≤ τ M 2 ≝ Caτ.

Задача 1.2.3. Покажите, что явная схема Эйлера обладает первым порядком аппроксимации (согласованности) на любой дважды непрерывно дифференцируемой функциию

1.2.9. Устойчивость.

Второе важное свойство, которым обладает явная схема Эйлера, называется устойчивостью и определяется так: если z ∈ S_τ и, кроме того, ||z||_τ и τ достаточно малы, то уравнение

Fτ(y) = z

(7)

однозначно разрешимо и существует такая не зависящая от τ и ||z||_τ константа C_s, что

||y – φτ||τ = ||Fτ–1(z)– φτ||τ ≤ Cs||z||τ.

(8)

Устойчивость разностной схемы означает, что малые возмущения z в начальных данных и правой части разностной схемы приводят к равномерно малому по τ изменению решения (напомним, что φτ — решение невозмущенной системы, а Fτ–1(z) — возмущенной). Поскольку φτ = Fτ–1(z),неравенство (8), переписанное в виде ||Fτ–1(z)– Fτ–1(0)||τ ≤ Cs||z|| τ, означает, в частности, непрерывность обратного к разностному оператору оператора Fτ–1в нуле.

Устойчивость — очень важное в приложениях свойство разностных схем. При практической реализации на ЭВМ разностных методов возникают, в частности, проблемы, связанные с невозможностью представления точных чисел в компьютере. В результате мы решаем не разностную схему (S), а несколько отличающееся от (S) уравнение. Все такие возмущения в разностной схеме, грубо говоря, можно "перенести в правую часть" и, таким образом, считать, что в ЭВМ ищется решение не разностной схемы (S), но решение возмущенного уравнения (7). Свойство устойчивости разностной схемы гарантирует близость при достаточно малых τ между точным (теоретическим) решением φτ разностной схемы и его практической реализацией Fτ–1(z)(где z — суммарный вектор возмущений). Источником возмущений служит не только невозможность точного представления данных в ЭВМ, но и неточность определения физических параметров модели, погрешность измерений и т.п.

1.2.10. Пример. Устойчивость явной схемы Эйлера.

Докажем, что явная схема Эйлера устойчива.

Разрешимость уравнения (7) для любых τ и z очевидным образом следует из того, что явная схема Эйлера является явной: значения yi решения y = Fτ–1(z) этого уравнения определяются рекуррентными формулами

y0 = x0 + z0,

yi = yi–1 + τf(ti–1, yi–1) + τzi,   i = 1, ..., n.

Обозначим y – φ_τ через ξ. Очевидно,

ξ0 = z0,

ξi = ξi–1 + τf(ti–1, yi–1) – τf[ti–1,(φτ)i–1] + τzi,   i = 1, ..., n.

Покажем теперь, что

||ξi|| ≤ (1 + τL)i· L + 1 L ||z||τ.

Для этого заметим сначала, что

||ξi|| = ||ξi–1 + τf(ti–1, yi–1) – τf[ti–1,(φτ)i–1] + τzi|| ≤

≤ ||ξi–1|| + τ||f(ti–1, yi–1) –f[ti–1,(φτ)i–1]|| + τ||zi|| ≤

≤ ||ξi–1|| + τL||yi–1 – (φτ)i–1|| + τ||z|| τ = (1 + τL)||ξi–1|| + τ||z|| τ.

Проведя такие оценки i раз, получим

||ξi|| ≤ (1 + τL)||ξi–1|| + τ||z|| τ ≤

≤ (1 + τL)[(1 + τL)||ξi–2|| +τ||z|| τ] + τ||z|| τ =

= (1 + τL)2||ξi–2|| + [(1 + τL) + 1]τ||z|| τ ≤ ...

... ≤ (1 +τL)i|| ξ0|| + [(1 + τL)i–1 + ... + (1 + τL) + 1]τ||z|| τ =

= (1 + τL)i|| ξ0|| +  (1 + τL)i – 1 (1 + τL) – 1 τ||z||τ ≤

≤ (1 + τL)i|| z|| τ +  (1 + τL)i– 1 L ||z|| τ =

=  (1 + τL)iL + (1+ τL)i – 1 L ||z||τ ≤ (1+τL)i· L + 1 L ||z||τ.

Воспользуемся теперь известным неравенством (1 + α)^1/α < e (напомним также, что τ = T/n):

(1 + τL)i ≤ (1 + τL)n = (1 + τL)[(TL)/(τL)] ≤ [(1 + τL)[ 1/(τL)]]TL < eTL.

Окончательно,

||Fτ–1z– φτ|| τ = ||y – φτ|| τ = ||ξ|| τ =  max 0≤i≤n ||ξi|| ≤

≤  max 0≤i≤n eTL·  L + 1 L ||z|| τ = eTL· L + 1 L ||z||τ ≝ Cs|| z|| τ.

Итак, явная схема Эйлера устойчива.

Покажем теперь, что из аппроксимации и устойчивости следует сходимость разностной схемы.

1.2.11. Теорема Лакса.

Любая устойчивая разностная схема k-го порядка аппроксимации на решении является схемой k-го порядка сходимости.

Д о к а з а т е л ь с т в о.  Действительно, если разностная схема имеет k-й порядок аппроксимации на решении, то ||Fτ(Pτφ)||τ ≤ Caτk и поэтому, в частности, при малых τ мала и ||Fτ(Pτφ)||τ. Следовательно, в силу устойчивости, Fτ–1[Fτ(Pτφ)] существует и ||Fτ–1[Fτ(Pτφ)]– φτ||τ ≤ Cs||Fτ(Pτφ)||τ. Но тогда, очевидно,

||Pτφ– φτ|| τ = ||Fτ–1[Fτ(Pτφ)]– φτ||τ ≤

≤ Cs|| Fτ(Pτφ)|| τ ≤ CsCaτ ≝ Cτk.

что и требовалось доказать.

Эта теорема описывает наиболее распространенный способ доказательства сходимости разностных схем.

Задача 1.2.4. Приведите пример не сходящейся разностной схемы, обладающей своством аппроксимации.

1.2.12. Немного о методах построения разностных схем.

Явная схема Эйлера может быть построена, исходя из различных соображений. Каждый из описываемых ниже приемов порождает ряд обобщений явной схемы Эйлера и может иллюстрировать основные методы построения разностных схем. В дальнейшем эти методы будут рассматриваться подробнее.

Попытаемся, отталкиваясь от уравнения (E), заменить его приближенным в том или ином смысле уравнением так, чтобы в результате получилась разностная схема. Первая идея выглядит так. Заменим в уравнении

x′(t) = f[t, x(t)]

(9)

производную x′(t) в точке t_i–1 ее приближенным значением [x(t_i) – x(t_i–1]/τ, а правую часть — ее значением в этой точке. В результате получим приближенное уравнение

x(ti) – x(ti–1) τ ≈ f[ti–1, x(ti–1)]

для отыскания значений точного решения уравнения (E) в точках сетки G_τ. Переход к сеточным функциям и замена приближенного равенства точным приводит к точному уравнению для приближенных значений решения, а именно, к явной схеме Эйлера. Использование других аппроксимаций производной в (9) (например, x′(t_i–1) ≈ [x(t_i+1) – x(t_i–1)]/2τ, а также других аппроксимаций правой части (например, f[t_i, x(t_i)]) взамен f[t_i–1, x(t_i–1)] позволяет получать другие разностные схемы.

Вторая идея основывается на замене дифференциального уравнения (9) интегральным

x(t + τ) = x(t) +  ∫ t+τ t f[s, x(s)]ds,

(10)

Если заменить в (10) t на t_i–1, а интеграл — приближенной квадратурной формулой (в данном случае прямоугольников), то мы получим приближенное уравнение

x(ti) ≈ x(ti–1) + τf[ti–1, x(ti–1)],

которое так же, как и выше приводит к явной схеме Эйлера. Если использовать другие квадратурные формулы (заменяя, например, интеграл на τf[t_i, x(t_i)] или τ[f(t_i–1, x(t_i–1)) + f(t_i, x(t_i))]/2), то будут получаться другие разностные схемы.

Третья возможность построения разностных схем связана с разложением решения в ряд Тейлора:

x(ti) = x(ti–1) + τx′(ti–1) +  τ2 2 x′′(ti–1) + ... .

"Обрежем" этот ряд до второго члена и выразим производную x′(t_i–1) из (9). В результате получим все то же приближенное уравнение

x(ti) ≈ x(ti–1) + τf[ti–1, x(ti–1)],

приводящее к явной схеме Эйлера. Удлинение отрезка ряда и другие аппроксимации коэффициентов приводят к другим разностным схемам.

Наконец, четвертая возможность связана с поиском решения в виде полинома. Допустим, мы ищем решение в виде полинома первого порядка:

ψ(t) = xi–1 + a·(t – ti–1)

с неизвестным коэффициентом a. Потребуем, чтобы этот полином точно удовлетворял уравнению (9) в некоторой точке t_i–1 + α:

ψ′(ti–1 + α) = a = f(ti–1 +α, xi–1 + aα).

Переходя к сеточным функциям, как и выше, получаем разностную схему:

xi = ψ(ti) = ψ(ti–1 + τ) = xi–1 + τf(ti–1 + α, xi–1 + aα).

При α = 0 это явная схема Эйлера. Если выбирать отличные от нуля α, а также брать полиномы более высоких порядков, то получается класс различных разностных схем.

File based on translation from T_EX by T_TH, version 3.05.
Created 23 May 2002, 20:10.