§ О2. Дифференциальные и интегральные неравенства

С одним примером интегрального неравенства мы уже сталкивались — это неравенство Гронуолла — Беллмана. Дифференциальные же неравенства — это оценки функций, удовлетворяющих неравенствам типа

y′(t) ≤ f[t, y(t)],   y(t0) ≤ x0

через решения задачи Коши

x′ = f(t, x),

(1)

x(t0) = x0.

(2)

Дифференциальные и интегральные неравенства широко используются для получения различных оценок. Важные приложения нам встретятся в очерках О3 и О4.

Сначала мы покажем какого типа бывают утверждения о дифференциальных (и интегральных) неравенствах в скалярном случае, а затем уже поясним как они могут быть перенесены на случай систем дифференциальных (и интегральных) неравенств.

Итак, пусть f: R×R → R — непрерывная функция.

Теорема о строгих дифференциальных неравенствах. Пусть непрерывно дифференцируемая на отрезке [t₀, t₀ + T] (T > 0) функция y удовлетворяет неравенствам

y′(t) < f[t, y(t)],   t ∈[t0, t0 + T],

(3)

y(t0) ≤ x0,

(2)

а x — определенное на [t₀, t₀ + T] решение задачи (1) – (2). Тогда при всех t ∈ (t₀, t₀ + T]

y(t) < x(t).

Для  д о к а з а т е л ь с т в а,  предположив противное, положим

τ = sup{s ∈ (t0, t0 + T]: y(ξ) < x(ξ) при всех ξ ∈ (t0, s)}

(см. рис. 1). Очевидно,

Рис. 1.

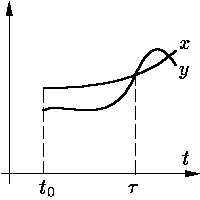
Но тогда

f[τ, x(τ)] = f[τ, y(τ)] > y′(τ) = lim h → 0 y(τ + h) – y(τ) h =

= lim h → 0–0 y(τ + h) – y(τ) h ≥ lim h → 0–0 x(τ + h) – x(τ) h = x′(τ) = f[τ, x(t)].

Противоречие.

Задача О2.1. Восстановите детали доказательства. В частности, почему: (а) τ > t₀?   (б) y(T) < x(T)?

Подчеркнем, что в некоторые моменты времени функция y может иметь бóльшую производную, чем функция x.

Задача О2.2. Приведите пример.

Если в (3) заменить строгое неравенство на нестрогое, то в случае единственности решения задачи (1) – (2) на отрезке [t₀, t₀ + T] заключение теоремы с заменой строгого неравенства на нестрогое остается верным. Если же решение задачи (1) – (2) не единственно, то это, очевидно, не так: например, два произвольных решения задачи (1) – (2) не могут быть связаны неравенством x(t) ≤ y(t).

Задача О2.3. Приведите пример задачи Коши, имеющей решения x и y, которые не связаны ни неравенством x(t) ≤ y(t), ни неравенством y(t) ≤ x(t).

Однако, если заменить в предыдущей теореме произвольное решение x на специально выбранное, а именно, верхнее, то такая модификация остается справедливой. Решение x_в задачи (1) – (2) на отрезке [t₀, t₀ + T] называется верхним, если для произвольного решения x этой задачи выполнено неравенство

x(t) ≤ xв(t), t ∈ [t0, t0 + T] ∩ D(x).

Аналогично определяется нижнее решение x_н задачи (1) – (2).

Задача О2.4. Покажите, что если все решения задачи (1) – (2) определены на отрезке [t₀, t₀ + T], то функции x_в(t) = sup{x(t): x ∈ W} и x_н(t) = inf{x(t): x ∈ W} (здесь W — множество решений задачи (1) – (2)) являются, соответственно, верхним и нижним решениями этой задачи.

Теорема о нестрогих дифференциальных неравенствах. Пусть непрерывно дифференцируемая на отрезке [t₀, t₀ + T] функция y удовлетворяет условиям

y′(t) ≤ f[t, y(t)], t ∈ [t0, t0 + T],

(5)

y(t0) ≤ x0,

(6)

а x_в — верхнее решение задачи (1) – (2), определенное на [t₀, t₀ + T]. Тогда при всех t ∈ [t₀, t₀ + T]

y(t) ≤ xв(t).

(7)

Схема д о к а з а т е л ь с т в а   этой теоремы такова. Рассмотрим последовательность задач Коши

x′ = fk(t, x),

x(t0) = x0,

где f_k(t, x) = f(t, x) + 1/k (k ∈ N₊). Можно показать, что при некотором τ > 0 и всех достаточно больших k эта задача разрешима на [t₀, t₀ + τ] (см. очерк О1). Обозначим ее решение через x_k. Тогда, поскольку очевидно

y′(t) < fk[t, y(t)],    t ∈ [t0, t0 + τ],

в силу теоремы о строгих дифференциальных неравенствах

y(t) < xk(t),  t ∈ (t0, t0 + τ].

(8)

Оказывается, из последовательности {x_k} можно выделить сходящуюся, причем ее предел обязательно является верхним решением x_в задачи (1) – (2). Переходя в (8) к пределу при k → ∞, получаем нужное неравенство (7) на промежутке [t₀, t₀ + τ]. Теперь нетрудно показать, что верхняя грань таких τ совпадает с T.

Эти теоремы остаются, как легко видеть, верными, если заменить все неравенства на противоположные: "<" на ">" и " ≤" на "≥" (во второй теореме при этом, естественно, верхнее решение надо заменить на нижнее).

В приложениях в качестве функции y, как правило, фигурирует модуль гладкой функции, в общем случае дифференцируемым не являющийся. Сформулированные теоремы допускают обобщение на случай негладких функций.

Через D*φ(t), D_*φ(t), *Dφ(t) и _*Dφ(t) обозначим, соответственно, так называемые правое верхнее, правое нижнее, левое верхнее и левое нижнее числа Дини :

D*φ(t) = lim h → 0+0 φ(t + h) – φ(t) h ,

D*φ(t) = lim h → 0+0 φ(t + h) – φ(t) h ,

*Dφ(t) = lim h → 0–0 φ(t + h) – φ(t) h ,

*Dφ(t) = lim h → 0–0 φ(t + h) – φ(t) h .

Очевидно производные числа Дини (конечные или бесконечные) определены для любой функции φ.

Задача О2.5. Докажите, что

D*|φ(t)| ≤ |D*φ(t)|.

Теорема о нестрогих дифференциальных неравенствах с производными числами. Пусть непрерывная функция y: [t₀, t₀ + T] → R при всех t ∈ [t₀, t₀ + T] удовлетворяет неравенствам

D*y′(t) ≤ f[t, y(t)], y(t0) ≤ x0,

(9)

а x_в — верхнее решение задачи (1) – (2), определенное на [t₀, t₀ + T]. Тогда y(t) ≤ x_в(t) при всех t ∈ [t₀, t₀ + T].

Условие (9) в этой теореме можно заменить на условие

*Dy′(t) ≤ f[t, y(t)], t ∈ [t0, t0 + T].

(10)

В силу очевидных неравенств D_*φ(t) ≤ D*φ(t) и _*Dφ(t) ≤ *Dφ(t) в (9) и (10) нижние производные числа можно заменить на верхние.

Доказательство сформулированной теоремы лишь деталями отличается от доказательства в случае гладких функций y.

Аналогично формулируется теорема о строгих дифференциальных неравенствах с производными числами.

Помимо верхнего и нижнего решений в интегральной воронке задачи Коши (т. е. во множестве всех ее решений) можно выделить еще два специальных решения, которые позволяют более тонко оценивать функции, удовлетворяющие нестрогим дифференциальным неравенствам, в случае, когда известно в какой точке нарушается "строгость" неравенства. Эти решения — так называемые верхнее Δ-решение и нижнее Δ_*-решение задачи (1) – (2) — определяются следующим образом: верхнее Δ-решение (соответственно, нижнее Δ_*-решение) — это наибольшее (наименьшее) среди таких решений задачи (1) – (2), при движении по которым вправо нельзя отойти (двигаясь, разумеется, только по решениям) вниз (вверх) нигде, кроме точки t = t₀ (см. рис. 2).

Рис. 2.

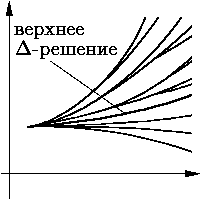
Формально определение, например, верхнего Δ-решения выглядит так. Пусть W — множество решений задачи (1) – (2) на отрезке [t₀, t₀ + T]. Для любых x ∈ W и τ ∈ [t₀, t₀ + T] определим функцию x_τ ∈ W равенством

xτ(t) = { x(t) при t ∈[t0, τ], xнτ(t)  при t ∈ [τ, t0 + T],

где x_нτ — нижнее решение уравнения (1), совпадающее в точке τ с x(τ), а затем для функции x ∈ W — функцию Δx равенством

(Δx)(t) = inf 0 ≤ τ ≤ T {xτ(t)}.

Верхнее Δ-решение — это наибольшее из решений задачи (1) – (2), удовлетворяющих равенству Δx = x.

Доказательство существования верхнего Δ-решения и нижнего Δ_*-решения достаточно сложно и мы его опускаем, отсылая читателя к специальной литературе.

Задача О2.6. Приведите пример задачи Коши, у которой верхнее, нижнее, верхнее Δ- и нижнее Δ_*-решения различны.

Теорема о строгих дифференциальных неравенствах на полуинтервале. Пусть непрерывно дифференцируемая на [t₀, t₀ + T] функция y удовлетворяет неравенствам

y′(t) < f[t, y(t)], t ∈ (t0, t0 + T], y(t0) ≤ x0.

Тогда при всех t ∈ (t₀, t₀ + T] выполнено неравенство y(t) < y_Δв(t), где y_Δв — верхнее Δ-решение задачи (1) – (2).

Иногда в приложениях бывает удобнее и проще получить оценку типа

y(t) ≤ y0 + ∫ t t0 f0[s, y(s)] ds,    t ∈ [t0, t0 + T],

(11)

нежели оценку типа (5). Из нее также вытекает оценка (7), правда, при дополнительных ограничениях на функцию f. Точнее, имеет место следующая

Теорема о нестрогих интегральных неравенствах. Пусть функция f является неубывающей по второму аргументу при любом фиксированном значении первого. Тогда из неравенств (11) и y₀ ≤ x₀ вытекает неравенство (7).

Доказывается эта теорема очень просто: обозначим правую часть неравенства (11) через z(t). Очевидно, y(t) ≤ z(t). Учитывая же монотонность f, получаем

z′(t) = f[t, y(t)] ≤ f[t, x(t)], t ∈ [t0, t0 + T].

Утверждение теоремы следует теперь из теоремы о нестрогих дифференциальных неравенствах.

Частным случаем этой теоремы является известная нам лемма Гронуолла — Беллмана: достаточно положить f(t, x) = L(t)y.

Аналогично формулируются и доказываются аналоги этой теоремы со строгими неравенствами, со строгими неравенствами на полуинтервале и т. п.

В заключение поясним, как утверждения о дифференциальных и интегральных неравенствах могут быть перенесены на многомерный случай. Будем говорить, что два вектора x, y ∈ Rⁿ связаны неравенством x < y (соответственно, x ≤ y), если x_i < y_i (соответственно, x_i ≤ y_i) при всех i = 1, ..., n (здесь x_i — i-ая координата вектора x). Функция f: R×Rⁿ → Rⁿ называется внедиагонально монотонной, если при любом i = 1, ..., n из условий x ≤ y, x_i = y_i (x, y ∈ Rⁿ) вытекает неравенство f_i(t, x) ≤ f_i(t, y) при всех t ∈ R.

Задача О2.7. Докажите, что если отображение (t, x) → f(t, x) монотонно по x (т. е. f(t, x) ≤ f(t, y), если x ≤ y), то оно внедиагонально монотонно, но, вообще говоря, не наоборот.

Например, теорема о системах строгих дифференциальных неравенств формулируется так. Пусть непрерывно дифференцируемая функция y: [t₀, t₀ + T] → Rⁿ удовлетворяет условиям

y′(t) < f[t, y(t)],    t ∈ [t0, t0 + T], y(t0) ≤ x0,

а x — определенное на [t₀, t₀ + T] решение задачи Коши (1) – (2) (в ней теперь f: R×Rⁿ → Rⁿ). Тогда y(t) < x(t) при всех t ∈ [t₀, t₀+T].

Подчеркнем, что в теоремах о системах интегральных неравенств требуется монотонность (а не только внедиагональная монотонность) функции f по x.

Литературные указания. Различные теоремы о дифференциальных и интегральных неравенствах встречаются во многих учебниках и монографиях по теории дифференциальных уравнений (см., напр., [Коддингтон — Левинсон, Хартман, Красносельский]). Монографии [ Мамедов — Аширов — Атдаев, Lakshmikantham — Leela, Rabczuk, Szarski, Walter] (см. также [Беккенбах — Беллман]) практически целиком посвящены неравенствам и их приложениям.

Задачи. О2.8. Пусть в теореме о строгих дифференциальных неравенствах неравенство (3) выполнено только при тех t, для которых x(t) = y(t). Докажите, что заключение теоремы остается в силе.

О2.9. Пусть x_i: [t₀, t₀ + T] → R (i = 1, 2) — решения задач Коши

x′ = fi(t, x),    x(t0) = x0,

где непрерывные функции f_i: [t₀, t₀ + T] × R → R связаны соотношением f₁(t, x) < f₂(t, x) при всех t, x. Докажите, что при всех t ∈ (t₀, t₀ + T]

x1(t) < x2(t).

О2.10. Пусть f_i: [t₀, t₀ + T] × R² → R (i = 1, 2) — непрерывные функции, f₁(t, x, y) не возрастает по y, а f₂(t, x, y) не убывает по x. Пусть непрерывно дифференцируемые на [t₀, t₀ + T] функции x = (x₁, x₂) и y = (y₁, y₂) удовлетворяют на этом отрезке неравенствам

{ x′1(t)≤ f1[t, x1(t), x2(t)], x′2(t)> f2[t, x1(t), x2(t)],      { y′1(t)> f1[t, y1(t), y2(t)], y′2(t)≤ f2[(t, y1(t), y2(t)]

и, кроме того, x₁(t₀) ≤ y₁(t₀), x₂(t₀) ≥ y₂(t₀). Докажите, что при всех t ∈ (t₀, t₀ + T]

x1(t) < y1(t),    x2(t) > y2(t).

О2.11. Сформулируйте и докажите аналог утверждения предыдущей задачи с производными числами Дини.

О2.12. Пусть f: [t₀, t₀ + T]×R → R — непрерывная ограниченная на всей области определения функция. Докажите, что задача Коши (1) – (2) имеет на отрезке [t₀, t₀ + T] верхнее и нижнее решения.

О2.13. Пусть x_k — решение задачи Коши

x′ = f(t, x) +  1 k ,   x(t0) = x0

на отрезке [t₀, t₀+T] (k ∈ N₊) и пусть последовательность {x_k} равномерно сходится на этом отрезке к функции x*. Покажите, что x* — верхнее решение задачи (1) – (2).

О2.14. Пусть все решения скалярной задачи Коши для уравнения (1) (f: [t₀, t₀ + T]×R → R) продолжимы на отрезок [t₀, t₀ + T]. Пусть непрерывно дифференцируемые на отрезке [t₀, t₀ + T] функции x и y удовлетворяют неравенствам

y′(t) ≤ f[t, y(t)], z′(t) ≤ f[t, z(t)],   t ∈ [t0, t0 + T], y(t0) ≤ x0,   z(t0) ≤ x0.

Пусть g: [t₀, t₀ + T]×R → R задается формулой

g(t, x) = f[t, max{x, y(t), z(t)}].

Докажите, что решение задачи Коши

x′ = g(t, x),   t ∈ [t0, t0 + T], x(t0) = x0

существует, удовлетворяет на [t₀, t₀ + T] неравенствам

x(t) ≥ y(t),   x(t) ≥ z(t)

и является решением уравнения (1).

О2.15. Пусть f такая же, как и в предыдущей задаче. Используя компактность множества решений задачи Коши (1) – (2) и результаты предыдущей задачи, докажите теорему существования верхнего решения этой задачи.

О2.16. Покажите, что если x: [a, b] → R — непрерывная функция и *Dx(t) ≤ 0 при всех t ∈ [a, b], то D*x(t) ≤ 0 при всех t ∈ [a, b].

О2.17. Используя теорему о нестрогих дифференциальных неравенствах с производными числами, докажите теорему о непрерывной зависимости решений от параметра.

О2.18. Пусть f: [t₀, t₀ + T]×R → R удовлетворяет условиям обобщенной теоремы Коши — Пикара. Пользуясь теоремой о нестрогих дифференциальных неравенствах с производными числами, докажите непрерывность разрешающего оператора для уравнения (1) по начальным данным.

О2.19. Пусть f такая же, как и в задаче 7. Обозначим через x_вi верхнее решение задачи Коши для уравнения (1), задаваемое начальным условием x(t₀) = x_i (i = 1, 2). Докажите, что если x₁ < x₂, то x_в1(t) < x_в2(t) при всех t ∈ [t₀, t₀ + T] (другими словами, верхнее решение монотонно зависит от начальных данных).

О2.20. Перенесите утверждение предыдущей задачи на системы дифференциальных уравнений.

О2.21. Покажите, что правая часть линейной системы уравнений

x′ = A(t)x + b(t)

внедиагонально монотонна в том и только том случае, когда внедиагональные элементы матрицы A(t) при каждом t неотрицательны: a_ij(t) ≥ 0 при i ≠ j и всех t.

О2.22. Пусть f: [t₀, t₀ + T]×R → R удовлетворяет условиям Каратеодори и x — верхнее решение Каратеодори на [t₀, t₀ + T] задачи Коши (1) – (2). Пусть абсолютно непрерывная функция y почти при всех t ∈ [t₀, t₀ + T] удовлетворяет неравенству

y′(t) ≤ f[t,y(t)].

Тогда, если y(t₀) ≤ x₀, то

y(t) ≤ x(t)

при всех t ∈ [t₀, t₀ + T].

О2.23. Перенесите утверждение предыдущей задачи на системы дифференциальных уравнений.

В следующих двух задачах описывается так называемый метод двусторонних приближений С.А. Чаплыгина. Предполагается, что в задаче Коши (1) – (2) функция f: [t₀, t₀ + T]×R → R непрерывна, ограничена, дважды непрерывно дифференцируема по второму аргументу и ∂²f(t, x)/∂x² > 0. Пусть непрерывно дифференцируемые на [t₀, t₀ + T] функции x_* и x* удовлетворяют дифференциальным неравенствам

(x*)′(t) > f[t, x*(t)],

x′*(t)< f[t, x*(t)]

при всех t ∈ [t₀, t₀ + T]. Определим функции g, G: [t₀, t₀ + T]×R³ → R равенствами

g(t, x, y, z) = f(t, z) + fx′(t, z)(x – z),

G(t, x, y, z) = f(t, z) + f(t, z) – f(t, y) z – y (x – z)

Определим теперь последовательности функций {x_k} и {y_k} на [t₀, t₀ + T] рекуррентными соотношениями:

x0 = x*,    y0 = x*;

функция x_k+1 есть решение задачи Коши (для линейного дифференциального уравнения)

x′ = G[t, x, xk(t), yk(t)],    x(t0) = x0,

а y_k+1 — задачи Коши

x′ = g[t, x, xk(t), yk(t)],    x(t0) = x0.

(Как можно геометрически интерпретировать эти решения?)

О2.24. Докажите, что если x — решение задачи (1) – (2) на [t₀, t₀ + T], то при всех t ∈ [t₀, t₀ + T]

yk(t) < yk + 1(t) < x(t) < xk+1(t) < xk(t), x′k(t) > f[t, xk(t)],    y′k(t) < f[t, yk(t)].

О2.25. Докажите, что

|xk(t) – yk(t)| ≤21–2k × sup s ∈ [t0, t0+T] | x*(s) – x*(s) |.

File based on translation from T_EX by T_TH, version 2.32.
Created 15 Jan 2000, 12:30.
Last modified 22 Apr 2002.