


| § 1.5. Анализ погрешностей | 
|
АНАЛИЗЪ м. греч. разборъ, раздробка, разрЂшенiе, разложенiе цЂлаго на составныя части его... Анализировать что, разлагать, разбирать цЂлое на начала, основы, стихiи...
Владимiр Даль.. Толковый словарь живаго великорусскаго языка
В этом параграфе описываются, с одной стороны, более тонкие и, с
1.5.1. Пример.
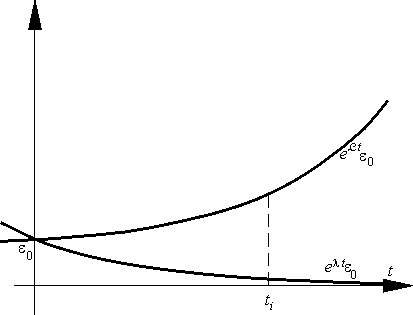
Оценка (16), фигурирующая в теореме о порядке сходимости одношаговых методов, в ряде случаев оказывается весьма грубой. Рассмотрим, например явный метод Эйлера для уравнения
| x′ = λx | (1) |
с λ = –103. Упомянутая оценка содержит быстро растущий с ростом T множитель
С другой стороны, в силу того, что уравнение (1) экспоненциально устойчиво, явный метод Эйлера обладает свойством уменьшения погрешности на каждом шаге. Для того чтобы понять это явление, рассмотрим простейшую ситуацию. Допустим мы ищем нулевое решение
уравнения (1) и обозначим через ε0 погрешность при выборе начального условия:
| εi = xi – 0 = xi–1 + λτxi–1 = (1 + λτ)xi–1 = (1 + λτ)(xi–1 – 0) = (1 + λτ)εi–1, | (2) |
откуда получаем
| εi = (1 + λτ)iε0. |
Так как λ < 0, при 0 < τ ≤ –2/λ множитель
1.5.2. В чем причина?
Суть этого явления, огрубляя ситуацию, можно описать так. При выводе оценки (2) мы считали, что погрешность с шага на шаг переносится, подчиняясь уравнению (1), а при выводе оценки
| ε′ = Lε, |
где L — константа Липшица функции Φ
Таким образом, метод, использованный при доказательстве теоремы 1.4.6, не учитывает более тонких свойств уравнения (E), а именно, свойств устойчивости. Поэтому мы сейчас сначала оценим погрешность на каждом шаге, а затем, учитывая свойства уравнения (E), оценим общую погрешность метода.
1.5.3. Локальная и глобальная погрешности.
Пусть (t, x) ∈ R×Rm — произвольная точка,
| xi = xi–1 + τΦ(ti–1, xi–1, τ). | (3) |
Локальной погрешностью метода (3) (в точке (t, x)) называется величина
| ε(τ) = ε(t, x, τ) = φ(t + τ) – (φτ)1 |
(рис. 6). Очевидно,
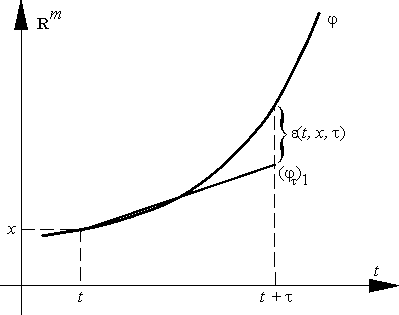
| ε(t, x, τ) = x + τρ(t, x, τ) – x – τΦ(t, x, τ) = τ[ρ(t, x, τ) – Φ(t, x, τ)] |
(напомним, что ρ(t, x, τ) = [φ(t + τ) – φ(t)]/τ, если τ > 0). Условие (1.4.15) в теореме 1.4.6 в точности означает, что
| ε(t, x, τ) ≤ Mτk+1. | (4) |
Как следует из примера п. 1.4.7, локальная погрешность характеризует свойства аппроксимации метода.
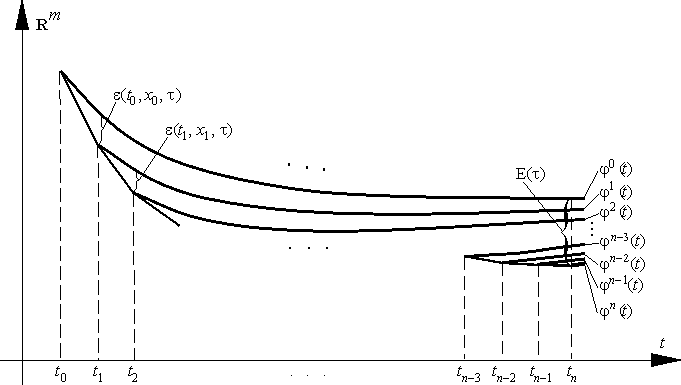
Глобальной погрешностью метода (3) называют величину
| En(τ) = φ(tn) – (φτ)n = φ(tn) – φτ(tn). |
Несколько огрубляя ситуацию, можно говорить, что в теореме 1.4.6 утверждается, что
|
В следующем пункте мы выведем более тонкую оценку глобальной погрешности через локальные.
Пусть φ — как обычно, решение задачи
уравнения (E), удовлетворяющее начальному условию
| (5) |
Оценим каждое слагаемое. Поскольку
| (φi–1)′(t) – (φi)′(t) ≡ f[t, φi–1(t)] – f[t, φi(t)]. | (6) |
Обозначим
Задача 1.5.1. Почему если
В этих обозначениях равенство (6) перепишется в виде
| (ψi)′(t) = ai(t)ψi(t), |
откуда
|
или
|
Поэтому, продолжая (5), получим
|
Именно второй множитель в каждом слагаемом содержит информацию о свойствах дифференциального уравнения, позволяющую оценивать как переносятся погрешности вдоль его решений. В самом деле, по теореме Лагранжа
| ai(s) = fx[s, ξi(s)], |
где ξi(s) ∈ (φi–1(s), φi(s)) и, таким образом,
|
(7) |
Например, если о функции f неизвестно ничего, кроме непрерывности и условия Липшица, то (см. п. 1.1.1)
|
Задача 1.5.2. Докажите, что из последней оценки
вытекает оценка
Задача 1.5.3. Как можно получить аналогичные
оценки в случае системы,
Более тонкие свойства уравнения используются для получения оценки глобальной погрешности в следующей теореме.
1.5.5. Теорема об оценке глобальной погрешности для устойчивого уравнения.
Пусть правая часть (скалярного) уравнения (E) дифференцируема по x и для некоторого Λ > 0 и всех (t, x) выполнено неравенство
| fx(t, x) ≤ –Λ. | (8) |
Пусть, кроме того, выполнена оценка (4) для локальной погрешности. Тогда
| (9) |
Д о к а з а т е л ь с т в о. В силу (8)
|
Поэтому, продолжая (7), с учетом (4), получаем
|
|
что и требовалось.
1.5.6. Замечания.
а) Оценка (9) в отличие от оценки (1.4.16) не ухудшается с ростом промежутка, на котором ищется решение.
б) (k+1)-й порядок малости по τ в правой части оценки (9) лишь кажущийся; на самом деле, поскольку
в) Условие (8) для скалярного уравнения в точности означает, что все решения уравнения (E) являются экспоненциально устойчивыми.
г) Аналогом условия (8) в многомерном случае
| Re λ ≤ –Λ |
при всех
1.5.7. Главный член локальной погрешности.
Условие (4) означает (при достаточной гладкости входящих в наши рассмотрения функций), что
|
Поэтому, раскладывая ε по степеням τ по формуле Тейлора до
| ε(t, x, τ) = h(t, x)τk+1 + O(τk+2). | (10) |
Величина h(t, x)τk+1 называется главным членом локальной погрешности. Она может быть вычислена через решение и его производные, а следовательно, через производные правой части.
Задача 1.5.4. Покажите, что для явного метода Эйлера
| (11) |
Найдите h(t, x) для метода предиктор-корректор
1.5.8. Задача контроля локальной погрешности.
При проведении вычислений весьма желательна информация о величине погрешности, вносимой на каждом шаге. С одной стороны, мы должны следить, чтобы погрешность не была слишком большой, чтобы в результате не получить решение с неудовлетворяющей нас точностью. С другой стороны, погрешность, следуя принципу
Теорема 1.4.6, а для устойчивых
1.5.9. Оценка локальной погрешности с помощью экстраполяции Ричардсона.
Нашей задачей является оценка выражения
| φ(t + τ) = (φτ)1 + h(t, x)τk+1 + O(τk+2). |
Обозначим для краткости h(t, x) через H:
| φ(t + τ) = (φτ)1 + Hτk+1 + O(τk+2). | (12) |
Погрешность же вычисления (φτ/2)2 складывается (см. (7)) из
"перенесенной" локальной погрешности
|
|
Заметим теперь, что в этой формуле (мы используем обозначение
| (13) |
| (14) |
| (15) |
Задача 1.5.5. Докажите формулы (13) – (15).
| (16) |
Отбрасывая в (12) и (16) члены
| φ~= (φτ)1 + h~τk+1, |
| φ~= (φτ/2)2 + h~τk+1/2k |
|
относительно неизвестных φ~и h~: |
|
|
|
Теперь величина h~τk+1может использоваться (с известной осторожностью) взамен главного члена погрешности |
File based on translation from
TEX by TTH,
version 3.05.
28 May 2002, 11: 10.