§ 1.6. Многошаговые методы

В этом параграфе описывается класс многошаговых методов.

1.6.1. Одношаговые и многошаговые методы.

Как уже говорилось, все рассмотренные выше методы являлись одношаговыми: для нахождения значения (φ_τ)_i приближенного решения φ_τ в точке t_i использовалось только значение (φ_τ)_i–1 приближенного решения в предыдущей точке t_i–1. Представляется вероятным, что использование дополнительной (уже имеющейся) информации, а именно, значений (φ_τ)_i–2, (φ_τ)_i–3, ..., позволит улучшить точность метода. Методы, использующие при вычислении (φ_τ)_i значения (φ_τ)_i–1, ..., (φ_τ)_i–p называются p-шаговыми методами. Подчеркнем, что пока не будет оговорено противное, мы предполагаем (это существенно), что сетка G_τ равномерная.

1.6.2. Явные методы Адамса.

Итак, допустим к настоящему моменту мы вычислили значения x_i–1, ..., x_i–p приближенного решения в узлах сетки t_i–1, ..., t_i–p. Уравнение (E) эквивалентно (см. п. 1.1.4) интегральному уравнению

x(t) = x(ti–1) +  ∫ t ti–1 f[s, x(s)] ds.

В частности, при t = t_i

x(ti) = x(ti–1) +  ∫ ti ti–1 f[s, x(s)] ds.

(1)

Не известную нам подынтегральную функцию s → f[s, x(s)] можно приблизить интерполяционным полиномом P, построенным по узлам t_i–1, ..., t_i–p, но поскольку нам неизвестны и значения f[t_j, x(t_j)] этой функции в узлах, при построении полинома P мы воспользуемся приближенными значениями, считая, что f[t_j, x(t_j)] ≈ f(t_j, x_j) (j = i – p, ..., i – 1). Тогда

x(ti) ≈ xi–1 +  ∫ ti ti–1 P(s) ds.

Таким образом, мы приходим к так называемому явному p-шаговому методу Адамса

xi = xi–1 +  ∫ ti ti–1 P(s)ds.

(2)

в котором P — интерполяционный полином, построенный по узлам t_i–1, ..., t_i–p и значениям f(t_i–1, x_i–1), ..., f(t_i–p, x_i–p).

Разумеется, (2) представляет собой лишь "заготовку" для метода. Конкретные методы получаются после вычисления коэффициентов интерполяционного полинома и интеграла.

Задача 1.6.1. Покажите, что явный одношаговый метод Адамса есть явный метод Эйлера

1.6.3. Пример: явный двухшаговый метод Адамса.

Интерполяционный полином P (в форме Лагранжа) в случае p = 2, очевидно, имеет вид

P(s) =  s – ti–2 ti–1 – ti–2 f(ti–1, xi–1) +  s – ti–1 ti–2 – ti–1 f(ti–2, xi–2).

Тогда, после несложных вычислений, учитывая, что t_i – t_i–1 = t_i–1 – t_i–2 = τ, получаем

∫ ti ti–1 P(s)ds =  τ 2 [3f(ti–1, xi–1) – f(ti–2, xi–2)].

Таким образом, явный двухшаговый метод Адамса имеет вид

xi = xi–1 +  τ 2 [3f(ti–1, xi–1) – f(ti–2, xi–2)].

(3)

Задача 1.6.2. Выведите явный трехшаговый метод Адамса

Обратим внимание на новое обстоятельство. Формула (3) неприменима при i = 1: для нахождения x₁ необходимо знать x_–1. Проблему "начального запуска" многошаговых методов мы обсудим чуть позднее.

1.6.4. Неявные методы Адамса.

Заметим, что при выводе явных методов Адамса мы использовали значения интерполяционного полинома P на отрезке [t_i–1, t_i]. Узлы же интерполяции лежат вне и, более того, по одну сторону от этого отрезка. Известно, что в таких случаях интерполяционный полином является плохим приближением. Чтобы избежать такой ситуации, добавим к нашим узлам интерполяции узел t_i и (неизвестное) значение f(t_i, x_i), обозначив получившийся полином через Q. В результате мы получим неявный p-шаговый метод Адамса

xi = xi–1 +  ∫ ti ti–1 Q(s)ds.

(4)

где Q — интерполяционный полином, построенный по узлам t_i–p, ..., t_i и значениям f(t_i–p, x_i–p), ..., f(t_i, x_i). Подчеркнем (ср. с явными и неявными методами Рунге — Кутты), что метод (4), в отличие от метода (3), не дает явной формулы для вычисления x_i, но представляет собой уравнение, которое должно быть разрешено относительно x_i.

Задача 1.6.3. Покажите, что в случае p = 0 получается неявный метод Эйлера.

Задача 1.6.4. Выведите неявные двух- и трехшаговые методы Адамса.

Явные методы Адамса часто называют методами Адамса — Бэшфорта, а неявные — методами Адамса — Мултона.

1.6.5. Линейные многошаговые методы.

Описанные выше методы укладываются в следующую общую конструкцию. Метод

p ∑ s = 0 αsxi–s = τ p ∑ s = 0 βs f(ti–s, xi–s)

(5)

называется линейным p-шаговым методом. Например, при p = 2, α₀ = 1, α₁ = –1, α₂ = 0, β₀ = 0, β₁ = 3/2, β₂ = –1/2 метод (5) представляет собой явный двухшаговый метод Адамса.

Методы (5) называются линейными, потому что в левой части стоит линейный оператор. Если β₀ = 0, то они называются (являются) явными, в противном случае — неявными. Мы всегда предполагаем, что α₀ ≠ 0 (чтобы x_i всегда фигурировал в уравнении (5)). Более того, не ограничивая общности, можно предполагать, что α₀ = 1. Коэффициенты α_s, β_s в (5) можно находить из разных соображений. Выше мы рассмотрели два таких приема.

1.6.6. Проблема "запуска" многошаговых методов.

Как уже отмечалось, формулы (2) так же, как и (4), (5), не являются разностными схемами (вернее, являются неполными разностными схемами), поскольку в них не заданы формулы (уравнения) для вычисления p начальных значений. Здесь нельзя просто положить, например, x_i = x⁰ при i = 0, ..., p – 1, поскольку эти значения будут аппроксимировать φ(t₀) только с точностью O(τ); если же сами методы являются методами высокого порядка точности, то перенесенная начальная погрешность сведет на нет все преимущества метода. Обычно поступают так. Либо насчитывают первые p значений с помощью одношагового метода того же порядка точности, либо используют методы более низкого порядка, но при этом используют более мелкий шаг, чтобы получить через соответствующее число шагов начальные значения с нужной точностью. Помимо всего прочего, необходимость в начальном запуске очевидно приводит в увеличению объема работы по программированию метода.

1.6.7. Сходимость многошаговых методов.

Без описания процесса запуска многошагового метода мы не можем воспользоваться определениями п. 1.2.6, поскольку в них фигурируют неопределенные начальные значения. Чтобы выделить свойства самогó многошагового метода безотносительно к выбору процедуры запуска, модифицируем определение сходимости многошаговых методов. Будем говорить, что метод (5) сходится с k-м порядком, если найдутся константы C₀ и C такие, что для любых решений φ задачи (E) – (C) и любых начальных значений (φ_τ)₀, ..., (φ_τ)_p–1, удовлетворяющих условию

||(φτ)i – (Pτφ)i|| ≤ C0τk,   i = 0, ..., p – 1,

выполнено неравенство

||φτ – Pτφ|| τ ≤ Cτk.

Другими словами, многошаговый метод сходится с k-м порядком, если, будучи запущенным из начальных значений, вычисленных с k-м порядком точности, он дает приближенное решение с k-м порядком точности.

1.6.8. Аппроксимация многошаговых методов.

При определении порядка аппроксимации многошаговых методов можно, как в п. 1.2.7, воспользоваться неравенством ||F_τP_τφ||_τ ≤ C_aτ^k, но для этого нужно будет определить разностный оператор F_τ на начальных значениях, т. е. опять привязаться к конкретной процедуре запуска. Здесь мы определим порядок аппроксимации в терминах локальной погрешности (ср. с п. 1.5.3). Локальной погрешностью линейного p-шагового метода (5) (в точке (t, x)) назовем величину

ε(t, x, τ) = φ(t + pτ) – (φτ)p,

где φ — решение уравнения (E), проходящее через точку (t, x), а φ_τ — приближенное решение, полученное методом (5) с точными начальными условиями

(φτ)0 = φ(t),   (φτ)1 = φ(t + τ),  ...,  (φτ)p–1 = φ[t + (p – 1)τ]

(6)

(рис. 8).

Рис. 8.

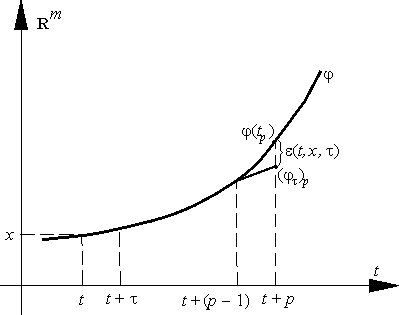
Говорят, что метод (5) является методом k-го порядка аппроксимации, если ||ε(t, x, τ)|| ≤ Cτ^k+1 с некоторой не зависящей от t, x и достаточно малых τ константой C; другими словами, если ε(t, x, τ) = O(τ^k+1) (ср.с (1.5.4)).

Локальная погрешность многошаговых методов выражается (также, как и для одношаговых) через f и коэффициенты метода. Для этого обозначим для любой дифференцируемой функции x: R → R^m агрегат

p ∑ s = 1 αs y(t – sτ) – τ p ∑ s = 1 βs y′(t – sτ)

через D(t, y, τ). Оказывается тогда, что в случае скалярного уравнения

ε(t, x, τ) =  D(tp, φ, τ) α0 –τβ0 fx(tp, Φ) ,

(7)

где Φ ∈ (φ(t +t_p), (φ_τ)_p), а φ — как и выше, решение уравнения (E), проходящее через точку (t, x).

Действительно, в силу (5) и (6) (φ_τ)_p удовлетворяет уравнению

p ∑ s = 1 αsφ(tp–s) + α0(φτ)p = τ p ∑ s = 1 βs f [ti–s, φ(ti–s)] + τβ0 f [tp, (φτ)p],

откуда, добавив и отняв α₀φ(t_p) – τβ₀ f [t_p, φ(t_p)] (= α₀φ(t_p) – τβ₀φ′(t_p)) и использовав введенное обозначение D, после несложных преобразований получим

D(tp, φ, τ) = α0[φ(tp) – (φτ)p] – τβ0(f[tp, φ(tp)] – f[tp, (φτ)p]) .

Применив к последнему слагаемому теорему Лагранжа, получим эквивалентное равенству (7) равенство

D(tp, φ, τ) = α0[φ(tp) – (φτ)p] – τβ0 fx(tp, Φ)[φ(tp) – (φτ)p] = = [α0 – τβ0 fx(tp, Φ)]ε(t, x, τ).

Задача 1.6.5. Выпишите D для явного и неявного двухшаговых методов Адамса.

Задача 1.6.6. Выведите аналог формулы (7) в многомерном случае.

Если отображение f ограничено, то поскольку α₀ = 1, знаменатель в (7) при достаточно малых τ равномерно отделен от нуля и поэтому ε(t, x, τ) и D(t_p, φ, τ) по τ являются бесконечно малыми одного порядка. Таким образом, метод (5) обладает k-м порядком аппроксимации, если и только если

D(t, y, τ) = O(τk+1)

(8)

для всех достаточно гладких функций y. Таким образом, последнее равенство можно рассматривать как эквивалентное определение порядка аппроксимации. Оно удобнее, поскольку в нем вообще не фигурируют решения дифференциального уравнения.

В следующем пункте мы приводим выраженный в терминах коэффициентов α_s и β_s признак выполнения равенства (8).

1.6.9. Теорема о порядке аппроксимации линейных многошаговых методов.

Для того, чтобы линейный p-шаговый метод имел k-й порядок аппроксимации для любой задачи Коши с k раз непрерывно дифференцируемой правой частью необходимо и достаточно выполнения следующих условий

p ∑ s = 0 αs = 0,    p ∑ s = 0 αs(p – s)j = j p ∑ s = 0 βs(p – s)j–1   (j = 1, ..., k)

(9)

(мы считаем здесь, что 0⁰ = 1).

Д о к а з а т е л ь с т в о.  Сохраним обозначение t_s = t + τs. Докажем (8) для всех k + 1 раз непрерывно дифференцируемых функций x. Подставим разложения

x(tp–s) =  k ∑ j = 0 (p – s)jτ j j! x(j)(t) + O(τk+1),

x′(tp–s) =  k–1 ∑ j = 0 (p – s)jτ j j! x(j+1)(t) + O(τk),

в определение D и преобразуем, используя очевидные свойства бесконечно малых O(τ^k+1) + O(τ^k+1) = O(τ^k+1),  λO(τ^k+1) = O(τ^k+1),  τO(τ^k) = O(τ^k+1):

D(tp, x, τ) =  p ∑ s = 0  αs ( k ∑ j = 0 (p – s)jτ j j! x(j)(t) + O(τk+1) )  –

–τ p ∑ s = 0  βs ( k–1 ∑ j = 0 (p – s)jτ j j! x(j+1)(t) + O(τk) )  =

=  p ∑ s = 0 αsx(t) +  p ∑ s = 0 αs  k ∑ j = 0 (p – s)jτ j j! x(j)(t) –

–  p ∑ s = 0 βs  k–1 ∑ j = 0 (j + 1) (p – s)jτ j+1 (j + 1)! x(j+1)(t) + O(τk+1) =

=  ( p ∑ s = 0 αs  ) x(t) + k ∑ j = 1 τ j j! x(j)(t)  ( p ∑ s = 0 αs(p – s)j – j p ∑ s = 0 βs(p – s)j–1 )  + O(τk+1).

Теперь эквивалентность соотношений (8) и (9) очевидна.

Например, для явного двухшагового метода Адамса, для которого (см. п. 1.6.5) α₀ = 1, α₁ = –1, α₂ = 0, β₀ = 0, β₁ = 3/2, β₂ = –1/2, соотношения (9) выполнены при j = 1, 2 и не выполнены при j = 3. Поэтому этот метод является методом второго порядка аппроксимации.

Задача 1.6.7. Покажите, что порядок аппроксимации явных p-шаговых методов Адамса равен p, а неявных — (p + 1).

1.6.10. Замечание о постоянном шаге.

Как уже отмечалось, недостатком многошаговых методов является необходимость специального начального запуска метода. Другим недостатком многошаговых методов является сложность процедуры перестройки длины шага, поскольку простые формулы получаются лишь в случае равномерной сетки. Обойти эту трудность можно разными способами. Во-первых, можно строить методы, рассчитанные на неравномерные сетки.

Задача 1.6.8. Постройте явный двухшаговый метод Адамса на неравномерной сетке.

Такие методы требуют пересчета коэффициентов на каждом шаге.

Второй способ заключается в интерполяции по полученным на неравномерной сетке значениям приближенного решения его значений на равномерной сетке (например, с помощью интерполяционных полиномов) и последующем применении многошагового метода с равномерным шагом к новым значениям.

Разумеется, все эти способы увеличивают объем вычислительной, а также программистской работы, усложняют логику программ и т. п.

File based on translation from T_EX by T_TH, version 3.05.
Created On 28 May 2002, 18: 26.
Last modified 8 May 2002.