§ 1.7. Устойчивость разностных схем

В отличие от схем Рунге — Кутты, многошаговые схемы устойчивы не всегда. В этом параграфе исследуются свойства устойчивости многошаговых схем.

1.7.1. Пример.

Рассмотрим явный линейный двухшаговый метод

xi – 3xi–1 + 2xi–2 = τ[f(ti–1, xi–1) – 2f(ti–2, xi–2)].

(1)

в применении к задаче Коши

x′ = 2t,   x(0) = 0.

Очевидно ее решением является функция φ(t) = t².

Задача 1.7.1. С помощью теоремы 1.6.9 покажите, что схема (1) является схемой первого порядка аппроксимации.

Начальный запуск схемы определим, положив

x0 = 0,   x1 = τ2

(таким образом, начальные данные совпадают с точным решением). Тогда, как нетрудно видеть, соответствующее сеточное решение задается формулой

(φτ)i = (2i + i2 – i –1)τ2 при i ≥ 2.

(2)

Задача 1.7.2. Проверьте.

Заметим теперь, что при достаточно малом τ

||φτ – Pτφ||τ =  max 2≤i≤n |(φτ)i – φ(ti)| =

= max 2≤i≤n |(2i + i2 –i – 1 – i2)τ2| = max 2≤i≤n |2i – i – 1|τ2 =

= (2n – n – 1)τ2 =  ( 2T/τ –  T τ  – 1 ) τ2 → ∞ при τ → 0.

Таким образом, схема (1) хотя и является аппроксимирующей, не является сходящейся. Дело здесь, разумеется, в ее неустойчивости. Попробуем понять это явление подробнее. Ответственным за несходимость решения (2) к точному решению является первое слагаемое. А источник его появления таков. Решение уравнения (1) по аналогии с линейным обыкновенным дифференциальным уравнением (а также с системой линейных алгебраических уравнений, каковой она собственно и является) можно искать в виде "общее решение линейного однородного уравнения + частное решение неоднородного", а первое из них в виде ζ ⁱ (ср. с нахождением решений линейных однородных дифференциальных уравнений с постоянными коэффициентами в виде e^λt = ζ ^t (здесь ζ = e^λ). Тогда для того чтобы сеточная функция ζ ⁱ была решением однородной схемы (1), нужно, чтобы

ζ i – 3ζ i–1 + 2ζ i–2 ≡ 0,

или, что эквивалентно,

ζ2 – 3ζ+ 2 = 0.

(3)

Таким образом, сеточная функция i → ζ ⁱ является решением однородной схемы (1), если и только если ζ — корень уравнения (3). Наличие у этого уравнения корня ζ = 2 и дает слагаемое, пропорциональное 2ⁱ, растущее при τ → 0.

1.7.2. Устойчивость. Наводящие соображения.

Рассмотрим линейный p-шаговый метод

p ∑ s = 0 αsxi–s = τ p ∑ s = 0 βs f(ti–s, xi–s).

(4)

Можно надеяться, поскольку нас интересует поведение решений при τ → 0, что это поведение характеризует однородная разностная схема

p ∑ s = 0 αsxi–s = 0,

(5)

получающаяся из (4) при τ → 0. Кроме того, эту надежду подтверждает аналогия с обыкновенными дифференциальными уравнениями. Будем искать решение уравнения (5) в виде экспоненциальной функции. Подставив x_i = ζ ⁱ в (5):

p ∑ s = 0 αsζ i–s =  ( p ∑ s = 0 αsζ p–s ) ζ i–p = 0,

получим, что сеточная функция i→ζ ⁱ является решением (5) в том и только том случае, если число ζ является корнем полинома

ρ(ζ) =  p ∑ s = 0 αsζ p–s.

Этот полином называется производящим полиномом метода (4). Более того, если ζ — корень характеристического полинома кратности l, то решениями (5) являются также сеточные функции i → i^jζ ⁱ с j = 0, 1,..., l – 1.

Задача 1.7.3. Докажите!

Очевидно, что i → i^jζ ⁱ ограничена по i в том и только в том случае, если либо |ζ| < 1, либо |ζ| = 1 и j = 0. Поэтому для для того чтобы однородная схема (5) не имела растущих при i → ∞ решений, нужно, чтобы корни производящего полинома лежали в (замкнутом) единичном круге комплексной плоскости C, причем те из них, которые лежат на границе круга, были простыми. Схемы, производящие полиномы которых удовлетворяют указанному свойству, называются схемами, удовлетворяющими корневому условию.

Отметим здесь же, что в силу теоремы 1.6.9 (см. условие (1.6.9)), если метод (4) является аппроксимирующим, то его производящий полином с необходимостью имеет единичный корень: ρ(+1) = ∑ps=0 αs = 0.

1.7.3. Теорема об устойчивости линейных многошаговых методов.

Для того чтобы схема (4) была устойчивой, необходимо и достаточно, чтобы соответствующая однородная схема (5) удовлетворяла корневому условию.

Д о к а з а т е л ь с т в о  необходимости нами, по существу, уже проведено. В самом деле, применение метода (4) к дифференциальному уравнению x′ = 0 приводит к однородной схеме (1). Поэтому, если она не удовлетворяет корневому условию (скажем, для определенности, имеет корень ζ такой, что |ζ| > 1), то у нее есть решение вида ζ ⁱ. Поэтому при произвольных малых z решение ψ_τ разностной схемы F_τx = z будет содержать слагаемое вида cζ ⁱ, а поэтому ||ψ_τ – φ_τ||_τ будет стремиться к бесконечности при i → ∞.

Доказательство достаточности сложнее, и мы его опускаем.

Задача 1.7.4. Восстановите детали доказательства.

Задача 1.7.5. Рассмотрите случай кратного равного по модулю единице корня.

Производящий полином p-шаговых методов Адамса (как явных, так и неявных) имеет вид ρ(ζ) = ζ ^p – ζ ^p–1. Поэтому они, очевидно, устойчивы.

1.7.4. Сходимость линейных многошаговых методов.

В силу теоремы 1.6.9 для того, чтобы линейный p-шаговый метод (4) обладал k-м порядком аппроксимации, нужно удовлетворить k + 1 условие (1.6.9) на коэффициенты метода. Свободных же параметров в методе (4) ровно 2p + 1 (напомним, что мы считаем α₀ = 1). Поэтому теоретически достижимый порядок аппроксимации линейного p-шагового метода равен 2p. Однако, оказывается, методы (4) высокого порядка обязательно оказываются неустойчивыми и, следовательно, несходящимися. Более точно, имеет место следующая

Теорема Далквиста. Пусть k — порядок сходимости линейного p-шагового метода. Тогда k ≤ p + 2, если k четно, k ≤ p + 1, если k нечетно, k ≤ p, если β₀ = 0 (т. е. если метод явный).

Эта теорема (доказательство которой мы опускаем) задает ограничение на порядок сходимости многошаговых методов. Линейные устойчивые p-шаговые методы (p+2)-го порядка аппроксимации (и, следовательно, сходимости) называются оптимальными.

1.7.5. Абсолютная устойчивость.

Обсуждавшееся выше понятие устойчивости гарантирует, что устойчивый метод хорошо работает лишь при τ → 0. При этом в конкретной ситуации при конкретном (даже весьма малом) τ погрешность может сильно возрастать с ростом i. В реальности же нам нужно знать поведение при данном конкретном τ. Поскольку трудно выяснить, заключается ли причина роста погрешности в неустойчивости метода или в неустойчивости самогó дифференциального уравнения, важно выделить свойства устойчивости метода, безотносительные к свойствам дифференциального уравнения. Здесь обычно поступают так. Вместо произвольного дифференциального уравнения рассматривают так называемое модельное уравнение

x′ = λx

(6)

с комплексным параметром λ. Мотивировка выбора уравнения (6) в качестве модельного такова. Во-первых, его предельная простота. Во-вторых, это уравнение "представляет" локальное поведение решение общего дифференциального уравнения (E) в следующем смысле. Решения уравнения (E) локально (в окрестности любой точки (t₀, x₀)) ведут себя как решения линеаризованного уравнения

x′ = fx(t0, x0)x

(7)

в окрестности нуля. В случае, когда жордановы клетки линейного оператора f_x(t₀, x₀) простые (т. е. имеют размерность 1×1) уравнение (7) невырожденной заменой переменных приводится к уравнениею с диагональной матрицей, на диагонали которой стоят собственные значения f_x(t₀, x₀), а получившееся уравнение распадается на систему уравнений вида (6) (случай не простых жордановых клеток не является случаем общего положения). Поэтому есть надежда, что по поведению решений разностного метода на уравнениях вида (6) можно с той или иной степенью достоверности предсказать их поведение на произвольных дифференциальных уравнениях.

Будем говорить, что метод (4) абсолютно устойчив при данном τ и данном λ ∈ C, если его глобальная погрешность E_n(τ) при применении его к уравнению (6) с данным λ при τ → 0 остается ограниченной.

1.7.6. Область абсолютной устойчивости.

Применение метода (4) к уравнению (6) приводит к разностной схеме

p ∑ s = 0 αsxi–s = τ p ∑ s = 0 βsλxi–s,

или

p ∑ s = 0 (αs – τλβs)xi–s = 0.

(8)

Соответствующее возмущенное уравнение имеет вид

p ∑ s = 0 (αs – τλβs)xi–s = τzi.

(9)

Как и в п. 1.7.2, общее решение неоднородного уравнения (9) складывается из общего решения однородного уравнения (8) и частного решения неоднородного уравнения (9). Частное решение можно считать малым. Поэтому поведение (9) определяется поведением решений однородного уравнения (8). Так же, как и выше, тривиально показывается, что функция ζ ⁱ является решением уравнения (8) в том и только том случае, если ζ является корнем полинома

πτλ(ζ) =  p ∑ s = 0 (αs – τλβs)ζ p–s,

называемого обычно полиномом устойчивости метода (4). Таким образом, если корни полинома лежат в единичном круге, то у уравнения (7) нет растущих решений (предоставляем читателю возможность произнести все нужные слова, относящиеся к корням, лежащим на границе круга).

По существу, мы показали, что если при данном τ и λ ∈ C все корни полинома устойчивости π_τλ лежат в единичном круге, то метод абсолютно устойчив при данных τ и λ. Множество S тех z ∈ C, при которых корни полинома устойчивости π_z лежат в единичном круге, называется областью абсолютной устойчивости метода (4). Другими словами, для того чтобы метод (4) был абсолютно устойчив при данных τ и λ, нужно, чтобы τλ ∈ S.

1.7.7. Пример: область устойчивости неявного метода Эйлера.

Полином устойчивости неявного метода Эйлера, очевидно, имеет вид

πz(ζ) = (1 – z)ζ– 1.

Его единственный корень — ζ = (1 – z)^–1. Он не превосходит по модулю единицы в том и только в том случае, если |z – 1| ≥ 1. Таким образом, S = {z ∈ C: |z – 1| ≥ 1} (рис. 9,а).

Рис. 9.

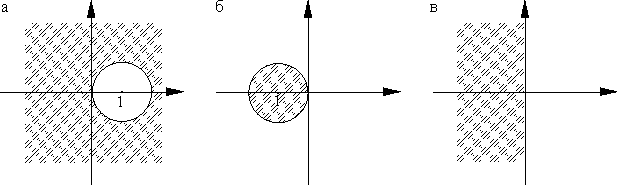
Задача 1.7.6. Докажите, что для явного метода Эйлера S = {z ∈ C: |z + 1| ≤ 1} (рис. 9,б), а для неявного одношагового метода Адамса S = {z ∈ C: Re z ≤ 0} (рис. 9,в).

1.7.8. Зачем нужно знать область устойчивости метода?

Тривиальный пример применения неявного метода Эйлера для нахождения нулевого решения задачи Коши

x′ = x,   x(0) = 0

показывает, что погрешность ε₀ в определении начального условия распространяется по закону

εi = (1 – τ)–iε0.

Очевидно, если шаг τ ∈ (0, 2), то погрешность растет по экспоненциальному закону с ростом i. Это происходит из-за того, что агрегат τλ (в данном случае равный τ) не лежит в области устойчивости метода.

Поэтому для контроля шага (особенно при применении одношаговых методов к системам малой размерности) иногда поступают так. Через некоторое число шагов находят матрицу Якоби f_x и все ее собственные значения, а затем корректируют шаг так, чтобы произведение шага на каждое собственное значение лежало в области устойчивости используемого метода. Эта процедура достаточно дорогостояща. Поэтому в случае больших размерностей ее обычно не применяют.

Кроме того, форма и размеры области абсолютной устойчивости важны при сравнении различных методов.

Несколько слов о нахождении области абсолютной устойчивости метода. Для простых случаев область может быть указана аналитически. В более сложных ситуациях применяют следующее рассуждение. Если точка z лежит на границе ∂S области S, то при этом z полином устойчивости π_zимеет корень ζ, равный по модулю единице: ζ = e^iα (здесь i — мнимая единица), т. е.

πz(eiα) = 0.

(10)

Решим при каждом α ∈ [0, 2π] уравнение (10) относительно z и обозначим его решение через z(α). С известными оговорками z(α) представляет собой параметризацию границы ∂S области устойчивости S или ее части.

File based on translation from T_EX by T_TH, version 3.05.
Created On 29 May 2002, 8: 37.