§ 1.8. Жесткие системы

Здесь описывается важный и часто встречающийся в приложениях класс так называемых жестких систем дифференциальных уравнений. Изучаются особенности численного решения жестких систем.

1.8.1. Пример. Рассмотрим систему дифференциальных уравнений

x′1= λ1x1,   x′2= λ2x2,

(1)

в которой λ₁ = –1, а λ₂ = –10⁶. Общее решение этой системы, как известно, имеет вид

x1(t) = c1e–t,   x2(t) = c2e–106t.

Допустим, нам нужно найти решение (1), удовлетворяющее начальным условиям

x1(0) = 1,   x2(0) = 1.

Воспользуемся, например, явным методом Эйлера. Поскольку его область устойчивости S (см. задачу 1.7.6) есть единичный круг в C с центром в точке –1, для устойчивого счета нужно, чтобы выполнялись неравенства

| λ1τ + 1| < 1,   | λ2τ + 1| < 1,

откуда следует, что τ должно быть меньше 2·10^–5. С другой стороны, при t > 5·10^–5 компонента x₂(t) решения отличается от нулевой функции менее, чем на ε = 10^–20 и, по-существу, второе уравнение после трех шагов длины τ = 2·10^–5 в решении не нуждается. Первая же компонента системы (1) может интегрироваться с шагом τ, выбранным из требования | λ₁τ + 1| < 1, т. е. с любым шагом τ < 2. Таким образом, за выбор шага при интегрировании системы (1) отвечает та компонента, поведение которой за исключением малых интервалов на оси t несущественно.

1.8.2. Жесткие системы.

Описанная выше ситуация возникает из-за большого разброса собственных значений матрицы системы (1): λ₂/λ₁ = 10⁶. Компонента с бóльшим (по модулю) собственным значением вынуждает выбирать мелкий шаг и, одновременно, быстро перестает влиять на решение. Класс дифференциальных уравнений с таким поведением выделяется в теории численных методов понятием жестких уравнений. Точнее, система линейных автономных дифференциальных уравнений

x′ = Ax

(2)

называется жесткой, если, во-первых, все собственные значения λ_i (i = 1, ..., m) матрицы A имеют отрицательную вещественную часть (т. е. система (2) экспоненциально устойчива) и, во-вторых,

S =  min 1≤i≤m Re λi max 1≤i≤m Re λi  >> 1.

Число S при этом называют коэффициентом жесткости системы (2). Значок >> ("значительно превосходит") на практике обычно означает, что S > 100, хотя часто встречаются задачи (например, в теории электрических цепей, в химической кинетике и т. п.) с коэффициентом жесткости ≈10⁶ и более.

В случае общей системы дифференциальных уравнений (E) жесткие системы можно выделять по-разному. Наиболее простым определением является, по-видимому, следующее. Пусть φ — решение уравнения (E) на отрезке [t₀, t₀ + T] и A(t) = ∂f(t, x)/∂x|_x=φ(t). Говорят, что система (E) жесткая вдоль решения φ на отрезке [t₀, t₀+T], если при всех s ∈ [t₀, t₀ + T] (автономная) система

x′ = A(s)x

жесткая.

Подчеркнем, что понятие жесткости относится к дифференциальному уравнению, а не к разностной схеме.

1.8.3. Еще один пример.

Попытаемся решить систему (1) неявным методом Эйлера. Как мы знаем (см. п. 1.7.7), его область устойчивости представляет собой внешность единичного круга в C с центром в точке +1: в частности, она содержит всю левую открытую полуплоскость {λ ∈ C: Re λ < 0}. Поскольку λ₁ и λ₂ в (1) отрицательны, λ₁τ, λ₂τ ∈ S при любом τ > 0. Таким образом, при использовании неявного метода Эйлера для решения устойчивой системы нет ограничений на величину шага, вызванных требованиями устойчивости метода.

1.8.4. A-устойчивые методы.

Как упоминалось выше, если область абсолютной устойчивости метода содержит левую открытую полуплоскость {λ ∈ C: Re λ < 0}, то для любой жесткой системы (2) метод абсолютно устойчив. В самом деле, поскольку для жестких систем Re λ_i < 0, произведение τλ_i лежит в S при любых τ > 0. Методы, область абсолютной устойчивости которых содержит левую открытую полуплоскость, называются A-устойчивыми. Для A-устойчивых методов шаг τ может выбираться только из соображений аппроксимации.

Однако, как оказалось, A-устойчивых методов не так уж много. А именно, доказано, что явных линейных многошаговых A-устойчивых методов (как, впрочем, и явных A-устойчивых методов Рунге — Кутты) просто нет. Порядок же аппроксимации неявного линейного A-устойчивого многошагового метода не может превышать двух.

Задача 1.8.1. Покажите, что метод трапеций

xi – xi–1 =   τ 2 [f(ti, xi) + f(ti–1, xi–1)]

является A-устойчивым методом второго порядка аппроксимации.

1.8.5. A(α)-устойчивые методы.

Из вышеизложенного следует, что требование A-устойчивости резко сужает класс доступных схем. Естественно попытаться снизить требования к области устойчивости метода. Один из возможных вариантов таков. Заметим, что если спектр σ(A) матрицы A лежит в левой открытой полуплоскости, в силу своей конечности, он лежит в некотором клине W_α = {λ ∈ C: |arg λ – π| < α}, где 0 ≤ α < π/2 (рис. 10).

Рис. 10.

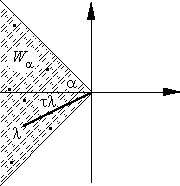
Поэтому, если область абсолютной устойчивости метода содержит клин W_α (такие методы называют A(α)-устойчивыми), то его применение к системе (2) с расположенным в W_α спектром не будет иметь ограничений на шаг из-за требований устойчивости.

Здесь доказано, что не бывает явных даже A(0)-устойчивых методов, но зато для любого 0 < α < π/2 существует неявный линейный многошаговый A(α)-устойчивый метод четвертого порядка аппроксимации.

Задача 1.8.2. Покажите, что неявный линейный четырехшаговый метод

xi –  48 25 xi–1 +  36 25 xi–2 –  16 25 xi–3 +  3 25 xi–4 = τ 12 25 f(ti, xi)

(3)

является методом четвертого порядка аппроксимации

Задача 1.8.3. Докажите, что метод (3) A(α)-устойчив при некотором α > 0.

Отметим, что если заранее известно, что решаемая (устойчивая) система дифференциальных уравнений имеет только вещественные (отрицательные в силу устойчивости) собственные значения (например, если матрица линеаризованной системы симметрична), то для устойчивого счета достаточно уже A(0)-устойчивости метода.

Подчеркнем еще раз, что поскольку, как уже отмечалось, не существует явных даже A(0)-устойчивых методов, для решения жестких задач могут применяться только неявные методы.

В заключение параграфа опишем еще один класс неявных линейных многошаговых методов, активно применяющихся при решении жестких задач.

1.8.6. Методы, основанные на дифференцировании.

В этих методах коэффициенты α_s, β_s линейного многошагового метода подбираются из следующих соображений (ср. c п. 1.2.12). Построим интерполяционный полином U(t) по узлам t_i–p, ..., t_i и значениям x_i–p, ... , x_i и потребуем, чтобы он удовлетворял уравнению (E) в точке t_i–r сетки, т. е. чтобы выполнялось равенство

U′(ti–r) = f(ti–r, xi–r).

(4)

Например, если p = 1 и r = 1, то

U(t) =  t – ti–1 ti – ti–1 xi +  t – ti ti–1 – ti xi–1

и после несложных преобразований равенство (4) превращается в явный метод Эйлера.

Если r = 1, то методы вида (4) явные, если же r = 0, то неявные. Эти методы при r = 0 называют еще формулами дифференцирования назад, поскольку в левой части равенства (4) стоит аппроксимация производной решения в точке t_i–r = t_i по узлам t_i–p, ..., t_i.

Задача 1.8.4. Выведите формулы дифференцирования назад для p = 1, 2, 3.

Задача 1.8.5. Исследуйте область абсолютной устойчивости построенных в предыдущей задаче методов.

При p = 1, 2 формулы дифференцирования назад являются A-устойчивыми, при p = 3, ..., 6 — A(α)-устойчивыми при некотором α > 0, при p > 6 они не являются даже A(0)-устойчивыми.

File based on translation from T_EX by T_TH, version 3.05.
Created 29 May 2002, 10: 24.