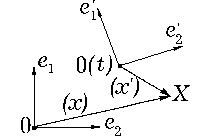1.4.8. Системы отсчета

Репером называется базис, состоящий из векторов единичной длины, исходящих из одной точки. Репер с часами называется системой отсчета. Пусть репер {e_i}, помещенный в точку 0 с часами, показывающими время t, некоторая (неподвижная) система отсчета. Зададим непрерывную кривую t → 0(t) и семейство непрерывно зависящих от t ортогональных преобразований O(t) с положительным определителем. Поместим теперь в точку 0(t) репер {e_i′} = {O(t)⟨e_i⟩} и часы, показывающие время t′ = t + α. Они образуют новую (подвижную) систему отсчета, которую мы будем обозначать (0(t), O(t), α). Поскольку ортогональные преобразования сохраняют углы и расстояния, можно представлять себе, что второй репер есть движущийся как обсолютно твердое тело первый. Точка X, задаваемая в первой системе отсчета радиус-вектором x, во второй системе отсчета задается радиус-вектором x′ (см. рис. 4.2).

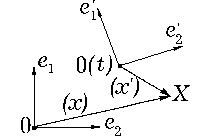
Рис. 4.2.

Найдем формулы перехода из одной системы отсчета в другую. Положим y = x – 0(t). Тогда

y = yiei = yiO–1(t)⟨ei′ ⟩ = yiO*(t)⟨ei′ ⟩ = yiαijej′,

где (α_i^j) — матрица преобразования O*(t) в базисе {e_i′}. Разложение же y по второму базису дает y = x′^je_j′. Откуда x′^j = α_i^jy ^j. Таким образом,

x′ = O*(t)⟨x – 0(t)⟩,    t′ = t + α.

Очевидно, если z = y – x — вектор с началом в точке x и концом в y в первой системе отсчета, то во второй системе отсчета представление соответствующего вектора имеет вид

z′ = O*(t)⟨z⟩.

Если A — линейное отображение векторов в первой системе отсчета, то во второй системе отсчета ему, как легко видеть соответствует линейное проебразование

A′ = O*(t)AO(t).

Скалярное s, векторное v и тензорное T поля на D по определению индифферентны (по отношению к изменению системы отсчета), если для любой подвижной системы отсчета (0(t), O(t), α)

s′(x′, t′) = s(x, t),

v′(x′, t′) = O*(t)⟨v(x, t)⟩,

T ′(x′, t′) = O*(t)ºT(x, t)ºO(t).