1.2.7. Основная теорема механики сплошной среды

Существует тензорное поле P: D → T²(R³) такое, что при всех ((x, t), n) ∈ D × S

pn(x, t) = P(x, t)⟨n⟩.

(7)

Д о к а з а т е л ь с т в о.  Зафиксируем произвольный ортонормированный базис {e_i} в R³ и точку (x, t) ∈ D. Если мы покажем, что для любого ν = νⁱe_i ∈ S

pν = νipei

(8)

(мы опускаем аргументы (x, t) у функции p_ν(x, t)), то на S искомый тензор P можно определить равенством (и опять (x, t) опускается)

P⟨ν⟩ = νi pei,

а после этого продолжить P с S на все R³ по линейности:

P⟨a⟩ = |a|P⟨ a |a| ⟩.

Докажем (8). Для этого мы используем интегральный закон сохранения импульса, переписанный в виде (6). Покажем сначала, что для любого ν ∈ S

pν = – p–ν.

(9)

Пусть Σ — плоскость, проходящая через точку x ∈ Ω_t с нормалью ν, y ∈ Σ ∩ Ω_t, B = B(y, ε) — шар в R³ с центром в y радиуса ε, целиком лежащий в Ω_t, B₁, B₂ — части этого шара, на которые он разбивается плоскостью Σ (B₂ и ν лежат по одну сторону от Σ), β = ∂B₁∩∂B₂ = B∩Σ (см. рис. 2.1).

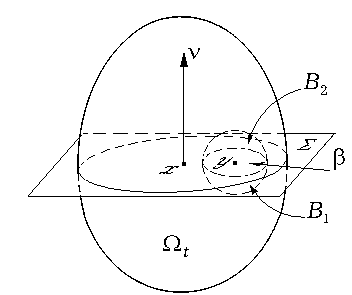
Рис. 2.1.

Запишем (6) для объемов B₁, B₂, B, сложим первые два из получившихся тождеств и вычтем третье:

( ∫∫ ∂B1  +  ∫∫ ∂B2  –  ∫∫ ∂B3 ) pn dω =

( ∫∫∫ B1  +  ∫∫∫ B2  –  ∫∫∫ B3 ) ρ ( dν dt  – f ) dω = 0.

В левой части этого равенства интегралы по границе шара B взаимно уничтожаются, а в оставшихся интегралах по β: в первом интеграле, очевидно, p_n = p_ν, а во втором — p_n = p_–ν. Таким образом,

∫∫ β [pν(y, t) + p–ν(y, t)] dσ = 0.

Поскольку β — произвольный круг, целиком лежащий в Ω_t ∩ Σ, а функция p_ν(y, t) + p_–ν(y, t) непрерывна, из леммы 1.2.3 следует (9).

Теперь докажем (8). Пусть ν = νⁱe_i таков, что все νⁱ отличны от нуля и, более того, положительны. Обозначим через Δ_ε тетраэдр, высекаемый из координатного угла (с началом в точке x) плоскостью, проходящей через конец вектора x + εν ортогонально ν, а также координатными плоскостями базиса, начало которого помещено в точку x (см. рис. 2.2).

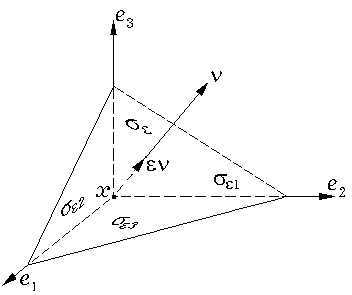
Рис. 2.2.

Пусть σ_ε — грань тетраэдра, перпендикулярная ν, а σ_εi — грани, перпендикулярные векторам e_i, соответственно. При достаточно малых ε этот тетраэдр целиком лежит в Ω_t. Применяя формулу (6) на Δ_ε, получаем

( ∫∫ σε  +  3 ∑ i = 1   ∫∫ σε1 ) pn dσ =  ∫∫∫ Δε ρ ( dν dt  – f ) dω,

или, учитывая, что n = ν на σ_ε и n = –e_i на σ_εi,

∫∫ σε pν dσ +  3 ∑ i = 1 ∫∫ σεi p–eidσ =  ∫∫∫ Δε ρ ( dν dt  – f ) dω.

(10)

Как легко видеть,

mes σε = ε2·mes σ1, mes σεi = ε2·mes σ1i, mes Δε = ε3·mes Δ1,

(11)

где mes σ – мера Лебега множества σ (в первых двух случаях плоская, т. е. площадь, а в последнем — объемная). Применим к (10) теорему о среднем значении:

pν(θε, t)·mes σε +  3 ∑ i = 1 p–ei(θεi, t)·mes σεi =

=  [ ρ ( dν dt  – f ) ] (Φε, t)·mes Δε

где θε ∈ σε, θεi ∈ σεi, а Φε ∈ Δε. Подставим (11) в последнее равенство, разделим на ε2 и перейдем к пределу при ε → 0, учитывая, что pν(θε, t) → pν(x, t), а p–ei(θεi, t) = p–ei(x, t) при ε → 0 (поскольку θε, θεi, Φε → x при ε → 0. Получим

(mes σ1)pν +  3 ∑ i = 1 (mes σ1i)p–ei = 0,

или, учитывая (9),

(mes σ1)pν –  3 ∑ i = 1 (mes σ1i)pei = 0,

Остается заметить, что mes σ_1i = mes σ₁cos(ν, e_i) = mes σ₁(ν·e_i) = mes σ₁νⁱ, и (8) в случае νⁱ > 0 доказано. Остальные случаи, когда νⁱ ≠ 0 разбираются аналогично. Наконец, в случае, когда один или два коэффициента νⁱ обращаются в нуль, равенство (8) следует из уже доказанного и непрерывности p.

Тензор P, существование которого утверждается в теореме, играет фундаментальную роль в механике сплошной среды и называется тензором напряжений. Саму теорему иногда называют теоремой Коши о существовании тензора напряжений. Существование этого тензора позволяет преобразовать поверхностный интеграл в законе сохранения импульса и момента импульса в объемный.