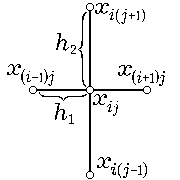| Глава II. Дискретные модели | § 2.2. Аппроксимации производных |
 | 2.2.6. Аппроксимации частных производных (оператор Лапласа) |  |
|
Пусть, как оговорено, |
|
Пусть |
|
Обозначим через |
|
Lh1°h2°u = Lh1°2(x1)u+Lh2°2(x2)u= = ux1–x1+ + ux2–x2+ (u ∈ F(Ωh1h2)). | (2) |
(Последнее выражение можно считать аналогом обозначения
| (Lh1°h2°u)(xij) = |
|
|
|
Заметим, что в точке xij значения оператора |