2.3.3. Задача Неймана для уравнения Пуассона

Рассмотрим в квадрате Ω = [0, X₁] × [0, X₂] указанную в названии пункта задачу Неймана для уравнения Пуассона

Δu = f(x),   x = (x1, x2) ∈ Ω,

(6)

∂u ∂n  = g(x),   x ∈ Γ.

(7)

В "операторном" виде она очевидно запишется в виде (3) — (4), (или, еще короче в виде (5)), если положить Lu = Δu, а lu = ∂u/∂n|_Γ. Аппроксимируем оператор Лапласа центральными разностями:

Lh°uh = fh ≝ Lh f;

здесь и ниже мы используем сокращенное обозначение h = (h1, h2), поэтому, в частности, Lh° = Lh1°h2°.

Займемся теперь аппроксимацией краевых условий. На нижней стороне квадрата Ω (мы считаем, для определенности, что ось Ox₁ горизонтальна, а Ox₂ вертикальна) это условие, очевидно, имеет вид

∂u(x1,x2) ∂(–x2) | x2 = 0 = – ∂u(x1,x2) ∂x2 | x2 = 0  = g(x1, 0)

(напомним, что n — это нормаль к Γ, направленная вне Ω). Для того, чтобы при аппроксимации производной, стоящей в этом краевом условии, использовались только точки, лежащие внутри Ω, можно воспользоваться, например, разностями вперед:

– ∂u(x1,x2) ∂x2 | x2 = 0  ≈ –ux2+ = – u(x1, h2) – u(x1, 0) h2 .

Теперь вспомним, что разности вперед аппроксимируют с погрешностью O(h2), тогда как дифференциальный оператор у нас аппроксимирован с погрешностью O(h12+ h22). Интуитивно ясно, что бóльшая погрешность в аппроксимации краевого условия должна привести к (по крайней мере) такой же погрешности в приближенном решении. (Эти априорные рассуждения позднее будут строго обоснованы в курсе "Методы вычислений".) Поэтому хотелось бы аппроксимировать краевое условие с тем же порядком погрешности. Здесь нельзя воспользоваться центральными разностями для аппроксимации первой производной в краевом условии, поскольку для их вычисления потребовались бы значения функции u в точках из CΩ, т. е. лежащих вне Ω (см. шаблон на рис. 3.1а). Поэтому воспользуемся следующей аппроксимацией первой производной произвольной функции φ

φ′(x) ≈  – φ(x + 2h) + 4φ(x + h) – 3φ(x) 2h

(см. шаблон на рис. 3.1б). Разложением в ряд Тейлора нетрудно показывается, что

| φ′(x) –  – φ(x + 2h) + 4φ(x + h) – 3φ(x) 2h |  ≤ M3h2.

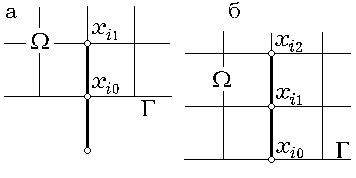
Рис. 3.1.

Поэтому на нижней стороне квадрата Ω краевое условие можно аппроксимировать, например, так

– –u(xi2) + 4u(xi1) – 3u(xi0) 2h  = g(xi0),   0 ≤ i ≤n.

(8)

На верхней границе квадрата для аппроксимации производной ∂u/∂n = ∂u(x₁, x₂)/∂x₂ по описанной схеме нужно взять разности, использующие значения в точках x_i(m–2), x_i(m–1) и x_im:

u(xi(m–2)) – 4u(xi(m–1)) – 3u(xim) 2h  = g(xim),   0 ≤ i ≤n.

(9)

Объединяя (8) и (9), также аналогичные краевые условия на правой и левой сторонах квадрата, запишем их в символической форме l_hu_h = g_h. Таким образом, краевая задача Неймана для уравнения Пуассона аппроксимируется следующей системой уравнений

Lhuh = fh, lhuh = gh,

которую в символической форме опять можно записать в виде

Lhuh = Fh.